エンタングルメントの動作

エンタングルメントの動作#

はじめに#

この授業では、基本的に重要な3つの例を見ていきます。最初の2つの例は、 テレポーテーションプロトコルと 超高密度符号 プロトコルで、主に送信者から受信者への情報の伝送に関係しています。3つ目の例は、 CHSHゲーム と呼ばれる抽象的なゲームで、量子情報における 非局所性 と呼ばれる現象を説明するものです。(CHSHゲームは必ずしもゲームとして説明されるわけではなく、実験として説明されることが多く、具体的には ベル テスト の一例であり、 CHSH 不等式 と呼ばれます。)

テレポーテーション、超高密度符号、CHSHゲームは、量子情報がどのように機能するかを説明するための単なる例ではありません（この点でも十分に役立っていますが）。むしろ、量子情報の基盤となる石のようなものです。3 つの例すべてでエンタングルメントが 重要な役割を果たしているため、この授業では、エンタングルメントの動作を確認し、エンタングルメントが非常に興味深く重要な概念である理由を探ります。これは、このシリーズでエンタングルメントについて探る最初の機会となります。

例自体に進む前に、3 つの例すべてに関連するいくつかの予備的なコメントを述べておきます。

アリスとボブ#

アリス と ボブ は、伝統的に、システム、プロトコル、ゲーム、および情報の交換を伴うその他の相互作用における仮想的な存在やエージェントに付けられた名前です。一般的に人間に付けられる名前ですが、抽象化されたものであり、必ずしも実際の人間ではないことを理解する必要があります。アリスとボブは複雑な計算を実行することが期待される場合もあります。

これらの名前は、1970年代に暗号技術の文脈で初めて使われましたが、それ以来、この慣習はより広く一般的になっています。アイデアは単純に、 (少なくとも世界の一部の地域では) 文字 A と B で始まる一般的な名前であるということです。また、簡潔にするために、アリスを「her」、ボブを「him」という代名詞で呼ぶのも非常に便利です。

デフォルトでは、アリスとボブは異なる場所にいると想像されます。彼らは、登場する文脈によって、異なる目標や行動をとることがあります。例えば、情報の伝達を意味する コミュニケーション では、送信者をアリス、受信者をボブと呼びます。一般的に、アリスとボブは典型的には協力し合っていることが多いですが、他の場面では競争していたり、異なる目標を持っていて一貫性があったり調和していなかったりするかもしれません。こうしたことは、その場の状況に応じて明確にしなければなりません。

必要に応じて、 チャーリー や ダイアン などの追加キャラクターを登場させることもできます。その他、盗聴者の イブ や悪意を持った人物の マロリー など、さまざまなペルソナを表す他の名前も使用されることがあります。

アリスとボブは、この授業で説明する 3 つの例すべてに登場し、以降の授業でも時折登場します。

リソースとしてのエンタングルメント#

エンタングルメントについて、いくつかの予備的なコメントをしておきます。

レッスン2の2量子ビットのエンタングルした量子状態の例を思い出してください：

\[ \vert \phi^+ \rangle = \frac{1}{\sqrt{2}} \vert 00\rangle + \frac{1}{\sqrt{2}} \vert 11\rangle. \tag{1} \]

これは 4 つのベル状態の 1 つであり、エンタングルした量子状態の典型的な例として見なされることがよくあります。

また、2ビットの確率的な状態のこの例もありました：

\[ \frac{1}{2} \vert 00 \rangle + \frac{1}{2} \vert 11 \rangle. \tag{2} \]

それは、ある意味で、エンタングルした量子状態 \((1)\) に似ています。これは、2 つのビットが相関している確率的な状態を表しますが、エンタングルしてはいません。エンタングルメントは、本質的に定義上、独自の量子現象です。簡単に言えば、エンタングルメントは 非古典的な 量子相関を指します。

残念ながら、エンタングルメントを非古典的な量子相関として定義することは、直感的なレベルではやや満足のいくものではありません。エンタングルメントとは何か、何が特別なのかを直感的な言葉で正確に説明するのが実際にはかなり難しいのは、このためかもしれません。

エンタングルメントの典型的な説明では、2つの状態 \((1)\) と \((2)\) を意味のある方法で区別することができないことがよくあります。例えば、2つのもつれた量子ビットの一方を測定すると、もう一方の量子ビットの状態も瞬時に影響を受けるとか、2つの量子ビットの状態を別々に記述できないとか、2つの量子ビットが互いの記憶を保持しているなどと言われることもあります。しかし、なぜエンタングルしていない状態 \((2)\) ではそうではないのでしょうか？この状態によって表される2つのビットは密接に繋がっており、それぞれが文字通りの意味でもう一方のビットを完全に記憶しています。しかし、それにもかかわらず、エンタングルされていないのです。

エンタングルメントを特別なものにし、状態 \((1)\) と状態 \((2)\) を非常に異なるものとして説明する一つの方法は、エンタングルメントを使って何ができるか、あるいはエンタングルメントのために何が起こるか説明することです。この説明は、ベクトルを使って状態に関する知識をどう表現するかの判断を超えています。この授業で取り上げる3つの例はすべて状態 \((1)\) でできることで、状態 \((2)\) を含む 全ての 古典的な相関のある状態ではできないことを説明しているという点で、この性質を備えています。

実際、量子情報と計算の研究では、エンタングルメントをさまざまなタスクを達成するためのリソースと見なすのが一般的です。このような場合、状態 \((1)\) はエンタングルメントの 1 つの 単位 を表していると見なされ、これを eビット と呼びます。 (「e」は「エンタングルメント」または「もつれ」を表します。状態 \((1)\) が 2 つの量子ビットの状態であることは事実ですが、それが表すエンタングルメントの量は 1 つの eビットです。)

ちなみに、確率的状態 \((2)\) をリソース、つまり、 共有されたランダム性 の 1 ビットとみなすこともできます。例えば、暗号化において、ランダムなビットを誰かと共有し（そのビットが何であるかは誰も知らないという前提で）、暗号化のための秘密鍵（または秘密鍵の一部）として使用することは、非常に有用です。しかし、この授業では、エンタングルメントに焦点を当て、エンタングルメントを使ってできることを紹介します。

用語の説明として、アリスとボブが eビットを共有する と言うとき、アリスは \(\mathsf{A}\) という名前の量子ビットを持ち、ボブは \(\mathsf{B}\) という名前の量子ビットを持っていて、このペア \((\mathsf{A},\mathsf{B})\) は量子状態 \((1)\) であるという意味です。 もちろん、量子ビットに別の名前をつけることもできますが、この授業では、わかりやすくするために、これらの名前を使うことにします。

1. テレポーテーション#

量子テレポーテーションとは、送信者（アリス）が受信者（ボブ）に量子ビットを送信する際に、2ビットの古典通信と1つの量子状態（eビット）を共有するプロトコルです。テレポーテーションという名称は、未来的なプロセスで物質をある場所から別の場所に運ぶというSFの概念を連想させるものですが、量子テレポーテーションでは物質はテレポートされず、実際にテレポートされるのは量子情報であることを理解する必要があります。

テレポーテーションの設定は次のとおりです。

アリスとボブはeビットを共有していると仮定します：アリスが量子ビット \(\mathsf{A}\) を持ち、ボブが量子ビット \(\mathsf{B}\) を持ち、ペア \((\mathsf{A},\mathsf{B})\) は \(\vert\phi^+\rangle\) の状態にあります。例えば、アリスとボブは過去に同じ場所にいて、状態 \(\vert \phi^+ \rangle\) の量子ビット \(\mathsf{A}\)　 と \(\mathsf{B}\) を用意し、それぞれが量子ビットを持って、それぞれの道を進んだという状況かもしれません。あるいは、この共有されたeビットを確立するために、第三者が関与するプロセスや複雑な分散プロセスなど、別のプロセスが用いられた可能性もあります。ただし、これらの詳細の環境は、テレポーテーション・プロトコルそのものには含まれていません。

アリスは、ボブに送信したい第3の量子ビット \(\mathsf{Q}\) を持っています。量子ビット \(\mathsf{Q}\) の状態は、アリスとボブにとって 未知 であると考えられ、それについての仮定はされません。つまり、例えば、量子ビット \(\mathsf{Q}\) は、アリスもボブもアクセスできない1つ以上の他の系とエンタングルしているかもしれません。アリスが量子ビット \(\mathsf{Q}\) をボブに送信したいということは、他の系と \(\mathsf{Q}\) の相関がどうであれ、アリスがボブに、プロトコルの開始時にアリスが持っていたのと同じ状態 \(\mathsf{Q}\) の量子ビットを持たせたいということです。つまり、まるでアリスからボブに \(\mathsf{Q}\) を物理的に渡したかのようにしたいということです。

もちろん、アリスが量子ビット \(\mathsf{Q}\) をボブに物理的に送り、 \(\mathsf{Q}\) が転送中に変化したり妨害されたりせずにボブに届くと仮定すれば、アリスとボブのタスクは達成されるものと考えることができます。しかし、テレポーテーションの設定では、前提として、アリスはボブに \(\mathsf{Q}\) を物理的に送ることはできません。ただし、古典的な情報をボブに送ることはできます。

これらは、様々な場面で合理的な仮定です。例えば、アリスがボブの正確な位置を知らなかったり、二人の間の距離が大きく離れていたりする場合、現在のまたは予測可能な未来の技術を使っても物理的に量子ビットを送ることは、控えめに言っても困難です。しかし、私たちが日常的に経験しているように、このような状況で古典的な情報伝達は非常に簡単です。

ここで、アリスとボブは、共有のeビットを使わずに、タスクを達成できるだろうか、と考える人がいるかもしれません。つまり、古典的な通信だけで量子ビットを伝送する方法はあるでしょうか？答えは「ノー」です。古典的な通信だけでは量子情報を伝送することはできません。このことは、本シリーズの第3回で取り上げた基本的な量子情報理論を使って証明することはそれほど難しくありませんが、とりあえず、古典通信だけで量子ビットを伝送する可能性を排除する直感的な方法として、複製不可能定理を考えてみましょう。

古典的な通信だけで量子情報を送信する方法があったとします。古典的な情報はコピーやブロードキャストが容易であるため、アリスからボブへの古典的な通信は、第二の受信者（仮にチャーリー）が受信する可能性があります。もしチャーリーがボブと同じ古典通信を受信したら、彼は量子ビットのコピー \(\mathsf{Q}\) を得ることができるのではないでしょうか？これは \(\mathsf{Q}\) が複製されることを意味しますが、複製不可能定理によるとこれは、不可能であることが既に分かっています。よって、古典的な通信だけでは量子情報を送ることはできない、という結論になります。

しかし、アリスとボブがeビットを共有するという前提があると、アリスとボブはタスクを遂行することが可能になります。これこそが、量子テレポーテーション・プロトコルです。

1.1 プロトコル#

下の図は、テレポーテーション プロトコルを説明する量子回路図です：

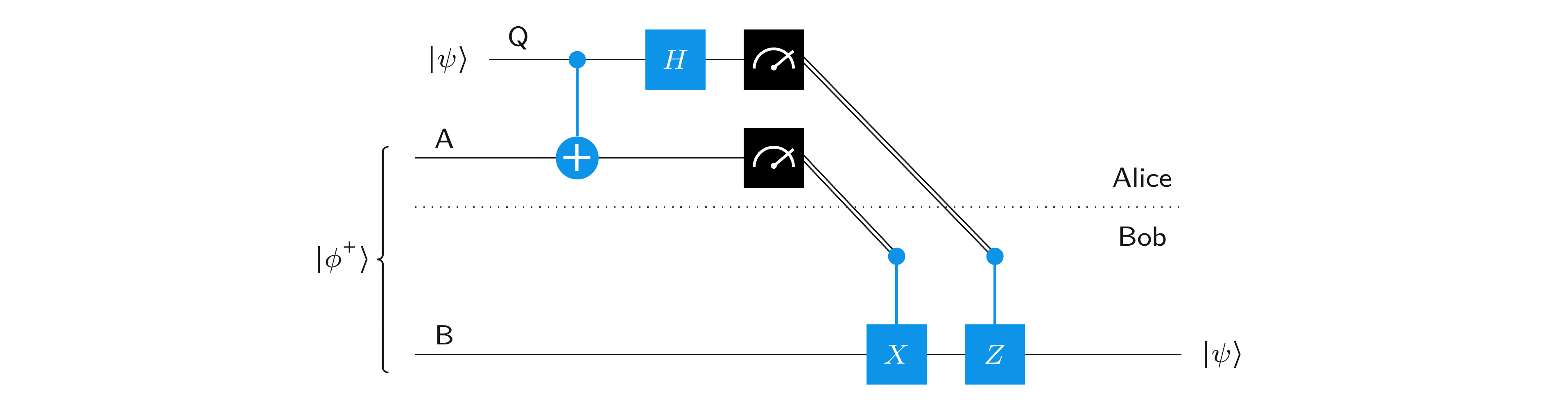
Teleportation circuit

この図は、アリスとボブの分離が描かれていて、斜めの2本の線がアリスからボブに送られる古典ビットを表している点で若干様式化されていますが、それ以外は普通の量子回路図です。

つまり、テレポーテーションのプロトコルは次のようなものです：

  1. アリスは、 \(\mathsf{A}\) を制御、\(\mathsf{Q}\) をターゲットとしてペア \((\mathsf{A},\mathsf{Q})\) に対して制御NOT演算を行い、 \(\mathsf{Q}\) に対してアダマール演算を実行します。

  2. その後、アリスは \(\mathsf{A}\) と \(\mathsf{Q}\) の両方を、標準基底で測定し、古典的な結果をボブに送信します。ここで、 \(\mathsf{A}\) の測定結果を \(a\) 、\(\mathsf{Q}\) の測定の結果を \(b\) と呼ぶことにします。

  3. ボブはアリスから \(a\) と\(b\) を受け取り、このビットの値によって、以下の演算を行います。

    • \(a = 1\) の場合、ボブは量子ビット \(\mathsf{B}\) にビットフリップ (または \(X\) ゲート) を実行します。

    • \(b = 1\) の場合、ボブは量子ビット \(\mathsf{B}\) に位相反転 (または \(Z\) ゲート) を実行します。

    つまり、 \(ab\) が \(00\) 、\(01\) 、\(10\) 、\(11\) のうちのどれかであることを条件として、ボブは量子ビット \(\mathsf{B}\) に演算 \(\mathbb{1}\) 、 \(Z\) 、 \(X\) 、\(ZX\) のいずれかを実行します。

これが、テレポーテーションプロトコルの完全な説明です。以下に示す分析は、これが実行されると、量子ビット \(\mathsf{B}\) が、プロトコルが実行される前の状態 \(\mathsf{Q}\) になることを示しています。これには、他のシステムとの相関関係も含まれます。つまり、このプロトコルは完全な量子ビット通信チャネルを効果的に実装しており、 \(\mathsf{Q}\) の状態が \(\mathsf{B}\) に「テレポート」されると言えます。

分析に進む前に、このプロトコルは \(\mathsf{Q}\) の状態の複製に成功していないことに注意してください。これは、複製不可能定理によって不可能であることが既にわかっています。 むしろ、プロトコルが終了すると、量子ビットの状態 \(\mathsf{Q}\) は、実行された測定の結果として、元の値から \(\vert b\rangle\) に変化します。 また、その過程でeビットが事実上「焼き尽くされた」ことにも注意してください: \(\mathsf{A}\) の状態は \(\vert a\rangle\) に変化し、もはや \(\mathsf{B}\) (または他のシステム) とエンタングルしていません。 これはテレポーテーションにかかるコストです。

1.2 分析#

テレポーテーションプロトコルを分析するために、量子ビット \(\mathsf{Q}\) が最初に状態 \(\alpha\vert 0\rangle + \beta\vert 1\rangle\) にある状況から始めて、上記の回路の動作を一度に 1 ステップずつ調べていきます。これは、 \(\mathsf{Q}\) が他のシステムとエンタングルしている可能性を考えていないため、最も一般的な状況ではありませんが、この単純なケースから始めると、分析が明確になります。以下では、単純なケースの分析に続いて、より一般的なケースについて説明します。

具体的には、次の図で示される時点での量子ビット \((\mathsf{B},\mathsf{A},\mathsf{Q})\) の状態を考えます：

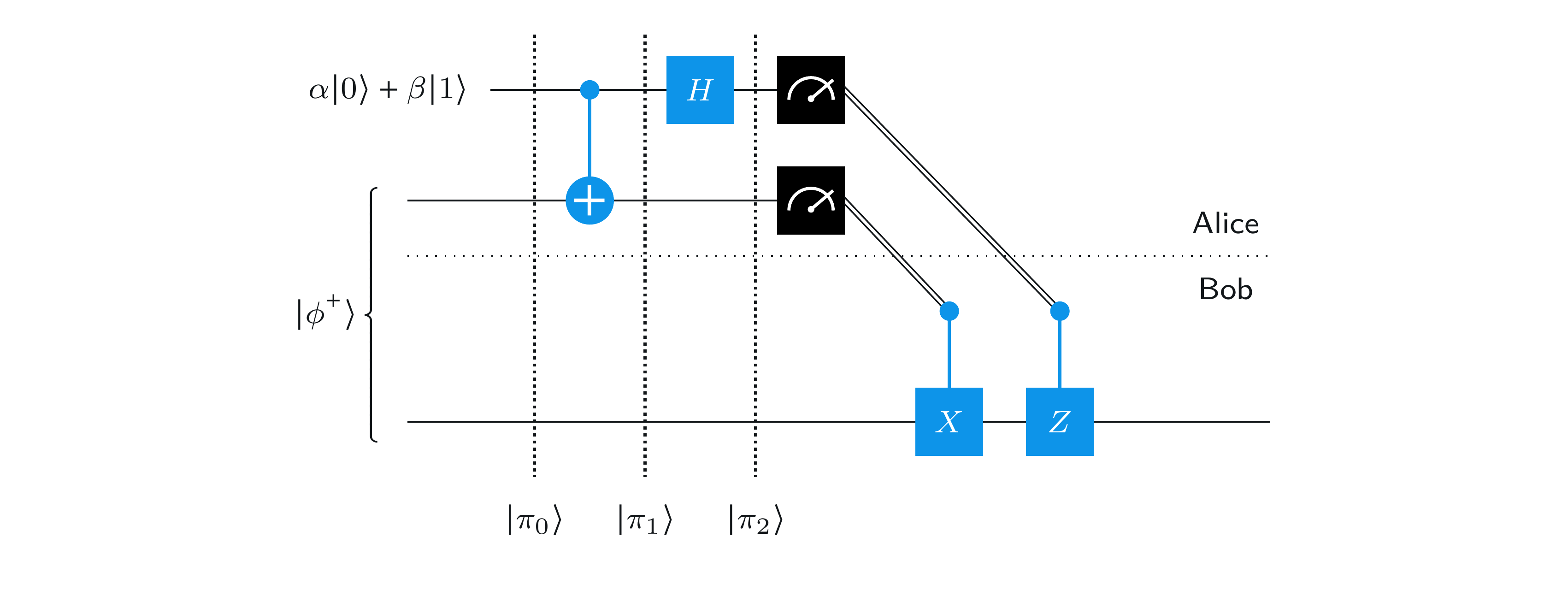
Teleportation circuit time-steps

量子ビット \(\mathsf{Q}\) が状態 \(\alpha\vert 0\rangle + \beta\vert 1\rangle\) でプロトコルを開始すると仮定すると、プロトコルの開始時の 3 つの量子ビット \((\mathsf{B},\mathsf{A},\mathsf{Q})\)の状態は、次のようになります。

\[ \vert \pi_0 \rangle = \vert \phi^+\rangle \otimes \bigl(\alpha\vert 0\rangle + \beta\vert 1\rangle \bigr) = \frac{\alpha \vert 000 \rangle + \alpha \vert 110\rangle + \beta \vert 001\rangle + \beta \vert 111\rangle}{\sqrt{2}}. \]

実行される最初のゲートは制御NOT ゲートで、状態 \(\vert\pi_0\rangle\) を次のように変換します。

\[ \vert \pi_1 \rangle = \frac{\alpha \vert 000 \rangle + \alpha \vert 110\rangle + \beta \vert 011\rangle + \beta \vert 101\rangle}{\sqrt{2}}. \]

次に、アダマールゲートが適用され、状態 \(\vert\pi_1\rangle\) を次のように変換します。

\[\begin{split} \begin{aligned} \vert\pi_2\rangle & = \frac{\alpha \vert 00\rangle \vert + \rangle + \alpha \vert 11\rangle\vert +\rangle + \beta \vert 01\rangle\vert -\rangle + \beta \vert 10\rangle\vert -\rangle}{\sqrt{2}}\\ & = \frac{\alpha \vert 000 \rangle + \alpha \vert 001 \rangle + \alpha \vert 110 \rangle + \alpha \vert 111 \rangle + \beta \vert 010 \rangle - \beta \vert 011 \rangle + \beta \vert 100 \rangle - \beta \vert 101 \rangle}{2}. \end{aligned} \end{split}\]

テンソル積の多重線形性を利用して、この状態を代わりに次のように書くことができます：

\[\begin{split} \begin{aligned} \vert\pi_2\rangle = \quad & \frac{1}{2} \bigl(\alpha\vert 0 \rangle + \beta \vert 1\rangle \bigr)\vert 00\rangle \\[1mm] + & \frac{1}{2} \bigl(\alpha\vert 0 \rangle - \beta \vert 1\rangle \bigr)\vert 01\rangle \\[1mm] + & \frac{1}{2} \bigl(\alpha\vert 1 \rangle + \beta \vert 0\rangle \bigr)\vert 10\rangle \\[1mm] + & \frac{1}{2} \bigl(\alpha\vert 1 \rangle - \beta \vert 0\rangle \bigr)\vert 11\rangle. \end{aligned} \end{split}\]

アリスからボブへの通信がまだ行われていないにもかかわらず、左端の量子ビット (つまり、下の量子ビット \(\mathsf{B}\) ) が数字 \(\alpha\) と \(\beta\) に依存しているように見えるため、一見すると、何か魔法のようなことが起こったように見えるかもしれません。実際、それは錯覚です。スカラーはテンソル積を介して自由に動くため、 \(\alpha\) と \(\beta\) は他の量子ビットよりも左端の量子ビットに多かれ少なかれ関連しています。代数を使用して、測定の分析を容易にするために状態を表現しただけです。

ここで、アリスの標準基底測定の結果の4つの考えられる場合について、その結果ボブが行う行動も合わせて考えてみましょう。

考えられる結果#

00#

アリスの測定結果は、以下の確率で \(ab = 00\) です。

\[ \Biggl\| \frac{1}{2}\bigl(\alpha \vert 0\rangle + \beta\vert 1\rangle\bigr) \Biggr\|^2 = \frac{\vert\alpha\vert^2 + \vert\beta\vert^2}{4} = \frac{1}{4}, \]

この場合、 \((\mathsf{B},\mathsf{A},\mathsf{Q})\) の状態は次のようになります。

\[ \bigl( \alpha \vert 0 \rangle + \beta \vert 1 \rangle \bigr) \vert 00 \rangle. \]

この場合、ボブは何もしないので、これがこの 3 つの量子ビットの最終状態です。

01#

アリスの測定結果は以下の確率で \(ab = 01\) です。

\[ \Biggl\| \frac{1}{2}\bigl(\alpha \vert 0\rangle - \beta\vert 1\rangle\bigr) \Biggr\|^2 = \frac{\vert\alpha\vert^2 + \vert{-\beta}\vert^2}{4} = \frac{1}{4}, \]

この場合、 \((\mathsf{B},\mathsf{A},\mathsf{Q})\) の状態は次のようになります。

\[ \bigl( \alpha \vert 0 \rangle - \beta \vert 1 \rangle \bigr) \vert 01 \rangle. \]

この場合、ボブは \(Z\) ゲートを \(\mathsf{B}\) に適用することで、 \((\mathsf{B},\mathsf{A},\mathsf{Q})\) を以下の状態にします。

\[ \bigl( \alpha \vert 0 \rangle + \beta \vert 1 \rangle \bigr) \vert 01 \rangle. \]

10#

アリスの測定結果は、以下の確率で \(ab = 10\) です。

\[ \Biggl\| \frac{1}{2}\bigl(\alpha \vert 1\rangle + \beta\vert 0\rangle\bigr) \Biggr\|^2 = \frac{\vert\alpha\vert^2 + \vert\beta\vert^2}{4} = \frac{1}{4}, \]

この場合、 \((\mathsf{B},\mathsf{A},\mathsf{Q})\) の状態は次のようになります。

\[ \bigl( \alpha \vert 1 \rangle + \beta \vert 0 \rangle \bigr) \vert 10 \rangle. \]

この場合、ボブは \(X\) ゲートを量子ビット \(\mathsf{B}\) に適用することで、\((\mathsf{B},\mathsf{A},\mathsf{Q})\) を以下の状態にします。

\[ \bigl( \alpha \vert 0 \rangle + \beta \vert 1 \rangle \bigr) \vert 10 \rangle. \]

11#

アリスの測定結果は、以下の確率で \(ab = 11\) です。

\[ \Biggl\| \frac{1}{2}\bigl(\alpha \vert 1\rangle - \beta\vert 0\rangle\bigr) \Biggr\|^2 = \frac{\vert\alpha\vert^2 + \vert{-\beta}\vert^2}{4} = \frac{1}{4}, \]

この場合、 \((\mathsf{B},\mathsf{A},\mathsf{Q})\) の状態は次のようになります。

\[ \bigl( \alpha \vert 1 \rangle - \beta \vert 0 \rangle \bigr) \vert 11 \rangle. \]

この場合、ボブは量子ビット \(\mathsf{B}\) に対して操作 \(ZX\) を実行しすることで、\((\mathsf{B},\mathsf{A},\mathsf{Q})\) を以下の状態にします。

\[ \bigl( \alpha \vert 0 \rangle + \beta \vert 1 \rangle \bigr) \vert 11 \rangle. \]

4つの場合のすべてで、ボブの量子ビット \(\mathsf{B}\) は、プロトコルの最後で状態 \(\alpha\vert 0\rangle + \beta\vert 1\rangle\) であることがわかります。これは、量子ビット \(\mathsf{Q}\) の最初の状態と同じです。これが私たちが示したかったことです: つまり、テレポーテーションプロトコルは全ての場合に正しく機能しました。

また、量子ビット \(\mathsf{A}\) と \(\mathsf{Q}\) は、アリスが取得した測定結果に応じて、それぞれ確率 \(1/4\) で4 つの状態 \(\vert 00\rangle\) 、 \(\vert 01\rangle\) 、 \(\vert 10\rangle\) 、 \(\vert 11\rangle\) のいずれかになることもわかります。つまり、すでに上で示唆されているように、プロトコルの最後で、アリスが持っている状態は、 \(\alpha \vert 0\rangle + \beta \vert 1\rangle\) ではなくなります。これは、複製不可能定理によって期待されていることです。

また、アリスの測定では、状態 \(\alpha \vert 0\rangle + \beta \vert 1\rangle\) に関する情報がまったく得られないことにも注意してください。つまり、 \(\alpha\) と \(\beta\) に関係なく、4つの可能な測定結果の確率はそれぞれ \(1/4\) です。これは、テレポーテーションが正しく機能するためにも不可欠です。未知の量子状態から情報を抽出すると、通常は必然的に量子状態が乱されますが、ここでは、ボブは乱されることなく状態を取得します。

ここで、量子ビット \(\mathsf{Q}\) が最初に別のシステム ( \(\mathsf{R}\) と名付けます) とエンタングルしている、より一般的な状況を考えてみましょう。上記と同様の分析により、テレポーテーションプロトコルがこのより一般的なケースで正しく機能することが明らかになります。プロトコルの最後に、ボブが保持する量子ビット \(\mathsf{B}\) は、 \(\mathsf{Q}\) がプロトコルの開始時にあったのと同じように \(\mathsf{R}\) とエンタングルします。まるでアリスがボブに \(\mathsf{Q}\) を渡したかのように。

これを証明するために、ペア \((\mathsf{Q},\mathsf{R})\) の状態が最初に次の形の量子状態ベクトルによって与えられると仮定します。

\[ \alpha \vert 0 \rangle_{\mathsf{Q}} \vert \gamma_0\rangle_{\mathsf{R}} + \beta \vert 1 \rangle_{\mathsf{Q}} \vert \gamma_1\rangle_{\mathsf{R}}, \]

ここで \(\vert\gamma_0\rangle\) と \(\vert\gamma_1\rangle\) は単位ベクトル、 \(\alpha\) と \(\beta\) は \(\vert \alpha \vert^2 + \vert\beta\vert^2 = 1\) を満たす複素数です。ペア \((\mathsf{Q},\mathsf{R})\) の任意の量子状態ベクトルは、上記のように表現できます。

次の図は、前と同じ回路に、システム \(\mathsf{R}\) (図の上部にある量子ビットの集合で表され、何も起こらない系)を追加したものです。

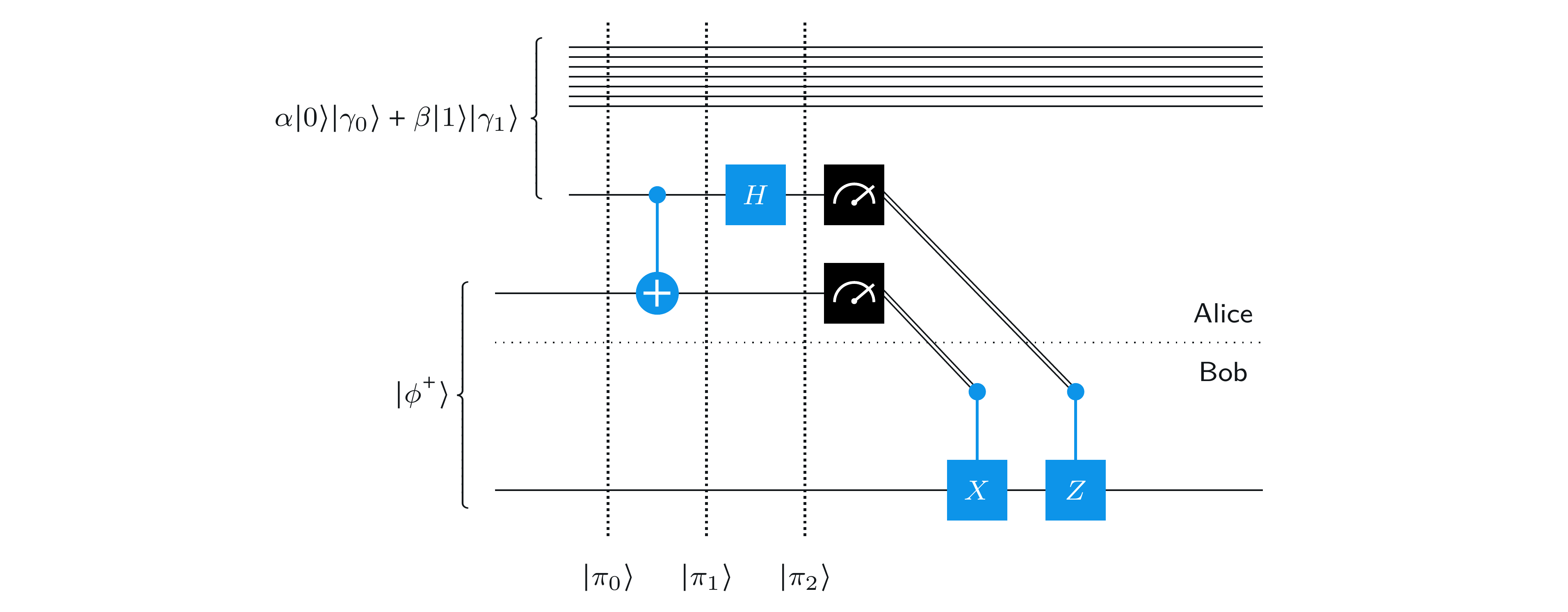
Teleportation with an entangled input

テレポーテーションプロトコルを実行したときに何が起こるかを分析するためには、レッスン2で説明したのと同じように、システムを順列化することが有効です。具体的には、 \((\mathsf{B},\mathsf{A},\mathsf{Q},\mathsf{R})\) ではなく、 \((\mathsf{B},\mathsf{R},\mathsf{A},\mathsf{Q})\) という順序でシステムの状態を考えます。この後の式では、わかりやすくするために、システムの名前を添え字として記載します。

プロトコルの開始時、これらのシステムの状態は次のとおりです：

\[\begin{split} \begin{aligned} \vert \pi_0\rangle & = \vert \phi^+\rangle_{\mathsf{BA}} \otimes \bigl( \alpha \vert 0\rangle_{\mathsf{Q}} \vert\gamma_0\rangle_{\mathsf{R}} + \beta \vert 1\rangle_{\mathsf{Q}}\vert\gamma_1\rangle_{\mathsf{R}}\bigr)\\[1mm] & = \frac{ \alpha \vert 0\rangle_{\mathsf{B}} \vert \gamma_0 \rangle_{\mathsf{R}} \vert 00 \rangle_{\mathsf{AQ}} + \alpha \vert 1\rangle_{\mathsf{B}} \vert \gamma_0 \rangle_{\mathsf{R}} \vert 10 \rangle_{\mathsf{AQ}} + \beta \vert 0\rangle_{\mathsf{B}} \vert \gamma_1 \rangle_{\mathsf{R}} \vert 01 \rangle_{\mathsf{AQ}} + \beta \vert 1\rangle_{\mathsf{B}} \vert \gamma_1 \rangle_{\mathsf{R}} \vert 11 \rangle_{\mathsf{AQ}}}{\sqrt{2}}. \end{aligned} \end{split}\]

最初に制御NOT ゲートが適用され、この状態が次のように変換されます。

\[ \vert\pi_1\rangle = \frac{ \alpha \vert 0\rangle_{\mathsf{B}} \vert\gamma_0 \rangle_{\mathsf{R}} \vert 00\rangle_{\mathsf{AQ}} + \alpha \vert 1\rangle_{\mathsf{B}} \vert\gamma_0 \rangle_{\mathsf{R}} \vert 10\rangle_{\mathsf{AQ}} + \beta \vert 0\rangle_{\mathsf{B}} \vert\gamma_1 \rangle_{\mathsf{R}} \vert 11\rangle_{\mathsf{AQ}} + \beta \vert 1\rangle_{\mathsf{B}} \vert\gamma_1 \rangle_{\mathsf{R}} \vert 01\rangle_{\mathsf{AQ}}}{\sqrt{2}}. \]

次に、アダマール ゲートが適用されます。上のより簡単な場合の分析と同様に、結果の状態を拡張および単純化すると、結果の状態は次の式になります：

\[\begin{split} \begin{aligned} \vert \pi_2 \rangle = \quad & \frac{1}{2} \bigl( \alpha \vert 0\rangle_{\mathsf{B}} \vert\gamma_0\rangle_{\mathsf{R}} + \beta \vert 1\rangle_{\mathsf{B}} \vert\gamma_1\rangle_{\mathsf{R}} \bigr) \vert 00\rangle_{\mathsf{AQ}}\\[1mm] + & \frac{1}{2} \bigl( \alpha \vert 0\rangle_{\mathsf{B}} \vert\gamma_0\rangle_{\mathsf{R}} - \beta \vert 1\rangle_{\mathsf{B}} \vert\gamma_1\rangle_{\mathsf{R}} \bigr) \vert 01\rangle_{\mathsf{AQ}}\\[1mm] + & \frac{1}{2} \bigl( \alpha \vert 1\rangle_{\mathsf{B}} \vert\gamma_0\rangle_{\mathsf{R}} + \beta \vert 0\rangle_{\mathsf{B}} \vert\gamma_1\rangle_{\mathsf{R}} \bigr) \vert 10\rangle_{\mathsf{AQ}}\\[1mm] + & \frac{1}{2} \bigl( \alpha \vert 1\rangle_{\mathsf{B}} \vert\gamma_0\rangle_{\mathsf{R}} - \beta \vert 0\rangle_{\mathsf{B}} \vert\gamma_1\rangle_{\mathsf{R}} \bigr) \vert 11\rangle_{\mathsf{AQ}}. \end{aligned} \end{split}\]

先ほどと同じように、アリスのありうる4つの測定結果と、それに対応するボブの実行を考えると、プロトコルの終了時に、 \((\mathsf{B},\mathsf{R})\) の状態は常に次のようになります。

\[ \alpha \vert 0 \rangle \vert \gamma_0\rangle + \beta \vert 1 \rangle \vert \gamma_1\rangle. \]

非公式に言えば、上の単純なケースと比較して、分析結果は大きく変わりません； \(\vert\gamma_0\rangle\) と \(\vert\gamma_1\rangle\) は、本質的に「一緒に来る」だけです。つまり、テレポーテーションは、量子ビット\(\mathsf{Q}\) の内容を \(\mathsf{B}\) に効果的に伝達し、他のシステムとの相関をすべて保持する、完璧な量子通信路を作ることに成功しました。

結局のところ、上の簡単なケースの解析を考えると、これは実は驚くべきことではないのです。その分析が明らかにしたように、私たちは任意の量子状態の量子ビットに対して恒等演算のように振る舞う物理的なプロセスを有しており、それが起こり得る方法はただ一つです。つまり、テレポーテーションが1つの量子ビットに対して正しく機能することが分かれば、プロトコルは完全でノイズのない量子チャネルを効果的に実装していると結論づけることができます。したがって、入力量子ビットが他のシステムとエンタングルしていても正しく機能するはずです。
この結論を正しく説明するには、量子情報の一般的な定式化が必要で、本シリーズのユニット3で取り上げますが、ポイントは、線形性によって、より一般的な分析をする必要がなかったということです。

1.3 さらなる議論#

ここで、テレポーテーションについて、簡単に結論を述べます。

まず、テレポーテーションは量子情報の 応用 ではなく、量子通信を行うためのプロトコルであることを理解する必要があります。量子通信が有用である限り有用です。

第二に、テレポーテーションが量子情報を伝達する標準的な方法になる日が来るかもしれないと推測することは合理的です。これは、おそらく エンタングルメント蒸留 と呼ばれるプロセスによるものになるでしょう。これは、ノイズの多い（あるいは不完全な）eビットを、より少ない高品質のeビットに変換するプロセスであり、ノイズのない、またはほぼノイズのないテレポーテーションに使用することができます。エンタングルメント蒸留のプロセスは、直接の量子通信ほどデリケートではないという考え方です。例えば、損失を受け入れることもできるし、プロセスがうまくいかなければ、またやり直せばいいのです。それに対して、実際に通信しようとする量子ビットは、もっと貴重なものなのかもしれません。

最後に、テレポーテーションの背後にあるアイデアとその仕組みは、量子情報と量子計算において非常に基本的なものです。量子情報理論の根幹をなすものであり、このアイデアのバリエーションもしばしば登場します。一例として、量子ゲートはテレポーテーションを利用して実装することができますが、初期状態や測定値が異なるため、通信するのではなく、選択した演算を適用することになるのです。

1.4 Qiskit での実装#

# Required imports

from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister
from qiskit_aer import AerSimulator
from qiskit.visualization import plot_histogram
from qiskit.result import marginal_distribution
from qiskit.circuit.library import UGate
from numpy import pi, random

ここでは、テレポーテーションプロトコルの量子回路実装を紹介します。

qubit = QuantumRegister(1, "Q")
ebit0 = QuantumRegister(1, "A")
ebit1 = QuantumRegister(1, "B")
a = ClassicalRegister(1, "a")
b = ClassicalRegister(1, "b")

protocol = QuantumCircuit(qubit, ebit0, ebit1, a, b)

# Prepare ebit used for teleportation
protocol.h(ebit0)
protocol.cx(ebit0, ebit1)
protocol.barrier()

# Alice's operations
protocol.cx(qubit, ebit0)
protocol.h(qubit)
protocol.barrier()

# Alice measures and sends classical bits to Bob
protocol.measure(ebit0, a)
protocol.measure(qubit, b)
protocol.barrier()

# Bob uses the classical bits to conditionally apply gates
with protocol.if_test((a, 1)):
    protocol.x(ebit1)
with protocol.if_test((b, 1)):
    protocol.z(ebit1)

display(protocol.draw("mpl"))
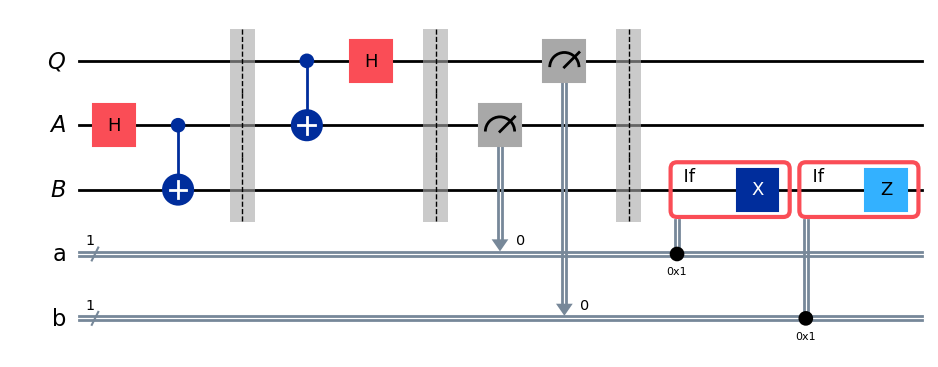
../../_images/b24c9f29e47ef9a0add7805958eac256f99ac9f155d4a0c944f380544b2a4a80.png

この回路では、Qiskitの機能のうち、barrier 関数と if_test 関数という、これまでの授業でまだ見ていない機能をいくつか使っていいます。 barrier 関数は、回路図を読みやすくするために視覚的に分離を行うもので、実際のハードウェア上で回路を実行する際には、コンパイルの際にQiskitがバリアを越えて簡略化や最適化を行わないという役割もあります。 if_test 関数は、古典ビットやレジスターに依存して条件付きで演算を適用するものです。

回路はまず \((\mathsf{A},\mathsf{B})\) を \(\vert \phi^+\rangle\) 状態に初期化し（プロトコル自体にはないですが）、続いてアリスの演算、アリスの測定、ボブの演算の順で行います。

プロトコルが正しく動作することを確認するために、初期化された \(|0\rangle\) 状態の \(\mathsf{Q}\) に対してランダムに生成された単一量子ビットゲートを適用し、テレポートするためのランダムな量子状態ベクトルを得ます。プロトコルを実行した後に、そのゲートの逆（すなわち随伴転置）を \(\mathsf{B}\) に適用することで、状態がテレポートされたことを確認できます。具体的には、状態が \(|0\rangle\) に戻ったかを測定します。

まず、ランダムにユニタリな単一量子ビットゲートを選択します。

random_gate = UGate(
    theta=random.random() * 2 * pi,
    phi=random.random() * 2 * pi,
    lam=random.random() * 2 * pi,
)

display(random_gate.to_matrix())

array([[ 0.93413463+0.j        ,  0.22680354+0.27559506j],
       [-0.04033827+0.35463405j,  0.78375333-0.50826984j]])

次に、テスト用の新しい回路を作成します。この回路は、まずランダムゲートを \(\mathsf{Q}\) に適用し、その後テレポーテーション回路を実行し、最後にランダムゲートの逆を量子ビット \(\mathsf{B}\) に適用して測定します。測定結果は確実に \(|0\rangle\) となるはずです。

# Create a new circuit including the same bits and qubits used in the
# teleportation protocol.

test = QuantumCircuit(qubit, ebit0, ebit1, a, b)

# Start with the randomly selected gate on Q

test.append(random_gate, qubit)
test.barrier()

# Append the entire teleportation protocol from above.

test = test.compose(protocol)
test.barrier()

# Finally, apply the inverse of the random unitary to B and measure.

test.append(random_gate.inverse(), ebit1)

result = ClassicalRegister(1, "Result")
test.add_register(result)
test.measure(ebit1, result)

display(test.draw("mpl"))
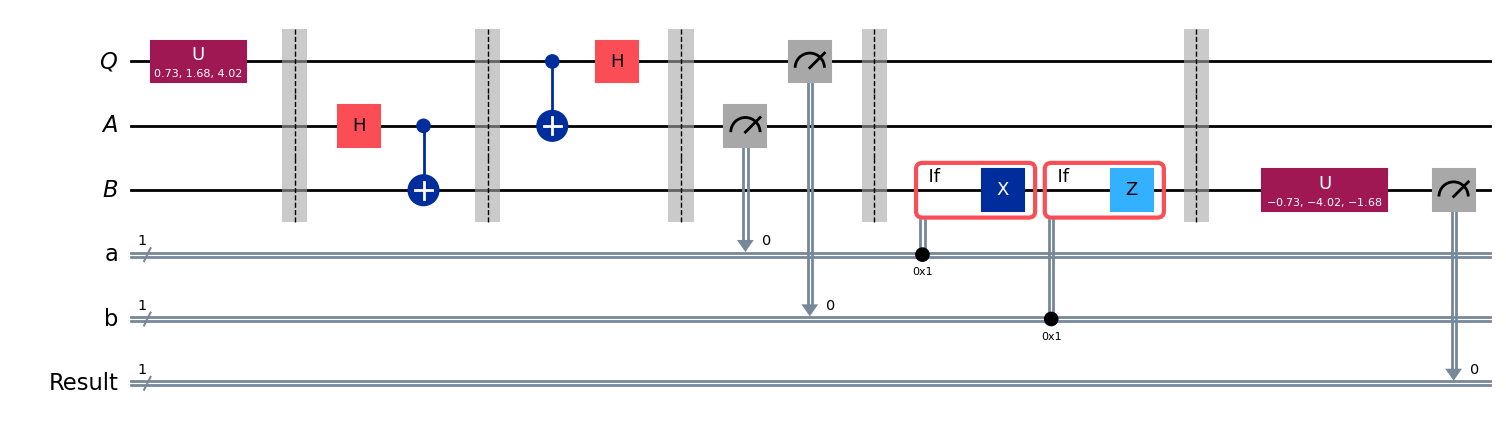
../../_images/25110da986f45e1765b6c8cca4ed0125ea34fcd46bf90071de94d0b944b627d9.png

最後に、この回路でAerシミュレーターを実行し、出力のヒストグラムをプロットしてみましょう。3つの古典ビットの統計データを見ることができます：一番下/左のビットは常に \(0\) であるべきで、これは量子ビット \(\mathsf{Q}\) が \(\mathsf{B}\) へのテレポートに成功したことを示し、一方他の2つのビットはほぼ均一です。

result = AerSimulator().run(test).result()
statistics = result.get_counts()
display(plot_histogram(statistics))
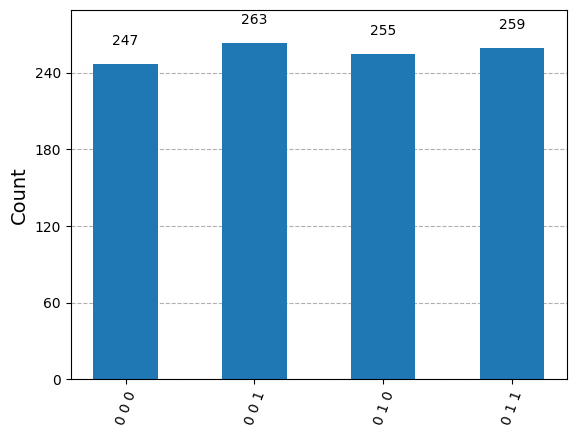
../../_images/086caf25f6e89c77d39cfbdf71d4b5ff2f935aeecedf1dd26ff4d6a6b1915556.png

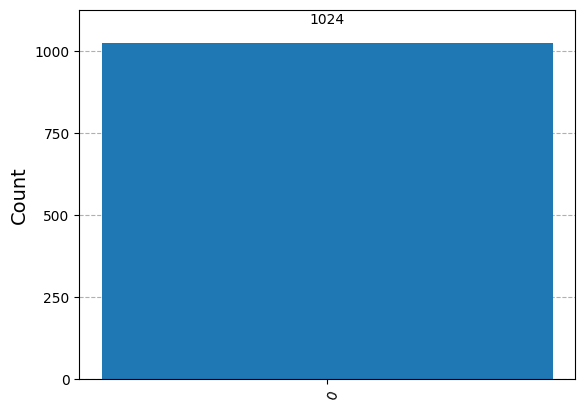
また、必要であれば、このようにテスト結果の量子ビットにのみフォーカスしてカウントをフィルタリングすることもできます：

filtered_statistics = marginal_distribution(statistics, [2])
display(plot_histogram(filtered_statistics))
../../_images/f31bdc5df75957bab956ed089ca9ecf7c70607102bcadd246b5b47ac791fecac.png

2. 超密度符号#

超高密度符号は、ある意味でテレポーテーションを補完するプロトコルです。1つの量子ビットを2つの古典ビットで伝送するのではなく（1eビットのエンタングルメントの犠牲を伴って）、1つの量子ビットで2つの古典ビットを伝送します（繰り返しますが、1eビットのエンタングルメントの犠牲を伴って）。

具体的には、送信者（アリス）と受信者（ボブ）が1eビットのエンタングルメントを共有するとします。この授業の慣習によれば、これは、アリスが量子ビット \(\mathsf{A}\) を、ボブが量子ビット \(\mathsf{B}\) を持ち、ペア \((\mathsf{A},\mathsf{B})\) は \(\vert\phi^+\rangle\) の状態にあります。アリスはボブに2つの古典ビット（ \(a\) と \(b\) とする）を送信したいと思っていて、1量子ビットを送信することでこれを達成しようとします。

テレポーテーションが達成する偉業よりも、こちらは面白くないと思うのが普通でしょう。量子ビットを送ることは、古典ビットを送ることよりもはるかに困難であり、1量子ビットの量子通信を2ビットの古典通信と交換し、さらに1eビットを犠牲にする超密度符号は、ほとんど価値がないように思われます。しかし、これは超密度符号が面白くないということを意味するものではなく、間違いなく面白いものです。

超密度符号が面白い理由の一つは、この授業のテーマにふさわしく、エンタングルメントを具体的に、（情報理論の文脈では）かなり印象的に使っているからです。量子情報理論において有名なホレボの定理は、共有されたエンタングル状態を用いなければ、1量子ビットを送信して1ビット以上の古典情報を伝達することは不可能であると言っています。(ホレボの定理自体は、これよりもさらに一般化されたものです。正確な記述は専門的で説明が必要ですが、これはその結果の一つです。)つまり、超高密度符号では、量子ビットを送ることで古典的な情報伝達能力を倍増させることができるのです。

超高密度符号が興味深いもう一つの理由は、テレポーテーションとの密接で補完的な関係であることです。これについては、このセクションの最後で詳しく説明します。

2.1 プロトコル#

次の量子回路図は、超高密度符号のプロトコルを示しています：

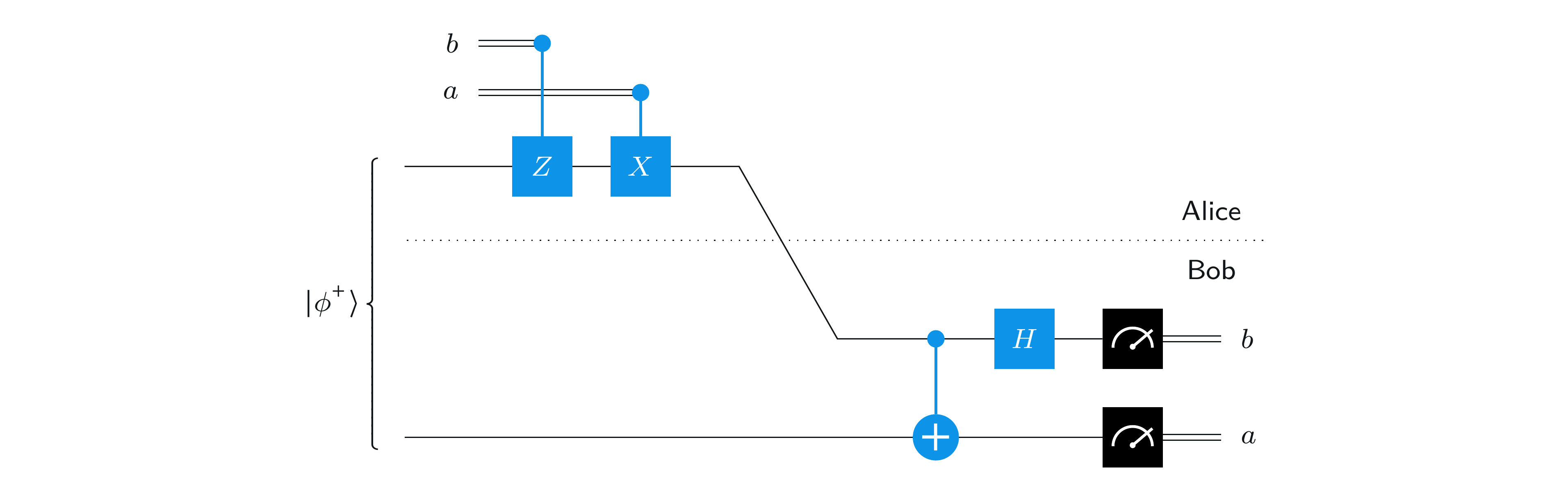
Superdense coding circuit

つまり、アリスが行うことは次のとおりです。

  1. アリスは最初に \(b=1\) かどうかを確認します。 \(b=1\) の場合、彼女は量子ビット \(\mathsf{A}\) に \(Z\) ゲートを実行します ( \(b=0\) の場合は実行しません)。

  2. アリスは \(a=1\) かどうかを確認します。 \(a=1\) の場合、彼女は量子ビット \(\mathsf{A}\) に \(X\) ゲートを実行します ( \(a=0\) の場合は実行しません)。

次に、アリスは自分の量子ビット \(\mathsf{Y}\) をボブに送信します。

量子ビット \(\mathsf{Y}\) を受け取ったときにボブは、まず、 \(\mathsf{Y}\) を制御、 \(\mathsf{X}\) をターゲットとして、制御NOT ゲートを実行します。そして、 \(\mathsf{Y}\) にアダマールゲートを適用します。次に、 \(\mathsf{X}\) を測定して \(a\) を取得し、 \(\mathsf{Y}\) を測定して \(b\) を取得します。どちらの場合も、標準基底で測定します。

2.2 分析#

このプロトコルの背後にある考え方は非常に単純です：アリスはどのベル状態をボブと共有したいかを選択し、ボブに自分の量子ビットを送り、ボブはアリスがどのベル状態を選択したかを測定します。

つまり、それらは最初に \(\vert\phi^+\rangle\) を共有し、ビット \(a\) および \(b\) に応じて、アリスはこの状態をそのままにしておくか、 \(\mathbb{1}\) 、 \(X\) 、 \(Z\) 、 \(XZ\) のいずれかを量子ビット \(\mathsf{A}\) に適用することによって、この状態を他のベル状態のいずれかにシフトさせます。

\[\begin{split} \begin{aligned} (\mathbb{1} \otimes \mathbb{1}) \vert \phi^+ \rangle = \vert \phi^+\rangle \\ (\mathbb{1} \otimes Z) \vert \phi^+ \rangle = \vert \phi^-\rangle \\ (\mathbb{1} \otimes X) \vert \phi^+ \rangle = \vert \psi^+\rangle \\ (\mathbb{1} \otimes XZ) \vert \phi^+ \rangle = \vert \psi^-\rangle \end{aligned} \end{split}\]

ボブの動作は、4つのベル状態に次のような影響を与えます：

\[\begin{split} \begin{aligned} \vert \phi^+\rangle \mapsto \vert 00\rangle\\ \vert \phi^-\rangle \mapsto \vert 01\rangle\\ \vert \psi^+\rangle \mapsto \vert 10\rangle\\ \vert \psi^-\rangle \mapsto -\vert 11\rangle\\ \end{aligned} \end{split}\]

上記は、それぞれの状態へのボブの演算を1つずつ計算することで、直接確認することができます。

よって、彼が測定を行うと、アリスがどのベル状態を選択したかを判断することができるのです。プロトコルが正しく動作することを確認するには、それぞれの場合をチェックする必要があります：

  • \(ab = 00\) の場合、ボブが \(\mathsf{A}\) を受け取ったときの \((\mathsf{B},\mathsf{A})\) の状態は \(\vert \phi^+\rangle\) です。ボブはこの状態を \(\vert 00\rangle\) に変換し、 \(ab = 00\) を取得します。

  • \(ab = 01\) の場合、ボブが \(\mathsf{A}\) を受け取ったときの \((\mathsf{B},\mathsf{A})\) の状態は \(\vert \phi^-\rangle\) です。ボブはこの状態を \(\vert 01\rangle\) に変換し、 \(ab = 01\) を取得します。

  • \(ab = 10\) の場合、ボブが \(\mathsf{A}\) を受け取ったときの \((\mathsf{B},\mathsf{A})\) の状態は \(\vert \phi^+\rangle\) です。ボブはこの状態を \(\vert 10\rangle\) に変換し、 \(ab = 10\) を取得します。

  • \(ab = 11\) の場合、ボブが \(\mathsf{A}\) を受け取ったときの \((\mathsf{B},\mathsf{A})\) の状態は \(\vert \phi^+\rangle\) です。ボブはこの状態を \(-\vert 11\rangle\) に変換し、 \(ab = 11\) を取得します (マイナス 1 の位相係数はここでは影響しません)。

2.3 Qiskit での実装#

# Required imports

from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister
from qiskit_aer.primitives import Sampler
from qiskit_aer import AerSimulator
from qiskit.visualization import plot_histogram

これは、送信するビットに応じて回路自体を指定する、超高密度符号の簡単な実装です。まず、送信するビットを指定しましょう。 (ビットを変えて、正しく動作することを確認してください。)

c = "1"
d = "0"

次に、それに応じて回路を作成します。ここでは、Qiskit が量子ビットにデフォルト名を使用できるようにします: 上の量子ビットは \(\mathsf{q}_0\) 、下の量子ビットは \(\mathsf{q}_1\) です。

protocol = QuantumCircuit(2)

# Prepare ebit used for superdense coding
protocol.h(0)
protocol.cx(0, 1)
protocol.barrier()

# Alice's operations
if d == "1":
    protocol.z(0)
if c == "1":
    protocol.x(0)
protocol.barrier()

# Bob's actions
protocol.cx(0, 1)
protocol.h(0)
protocol.measure_all()

display(protocol.draw("mpl"))
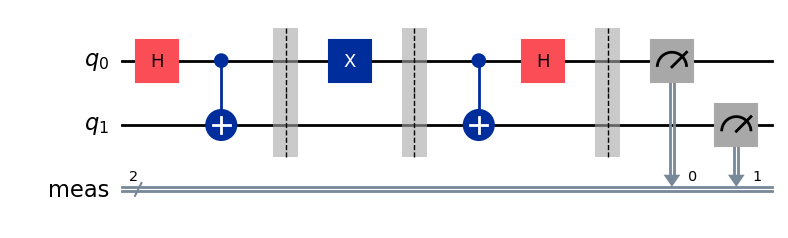
../../_images/a9f08f6efa405d8b50246db2b5be0d0fb2d71c04a8b2f8c8fedbf82245f7d955.png

measure_all 関数は、すべての量子ビットを測定し、その結果をそれぞれ1つの古典レジスターに格納します（したがって、この場合は2ビットを持つことになります）。

Aerシミュレーターを実行すると、期待通りの出力が得られます。

result = Sampler().run(protocol).result()
statistics = result.quasi_dists[0].binary_probabilities()

for outcome, frequency in statistics.items():
    print(f"Measured {outcome} with frequency {frequency}")

display(plot_histogram(statistics))

Measured 10 with frequency 1.0
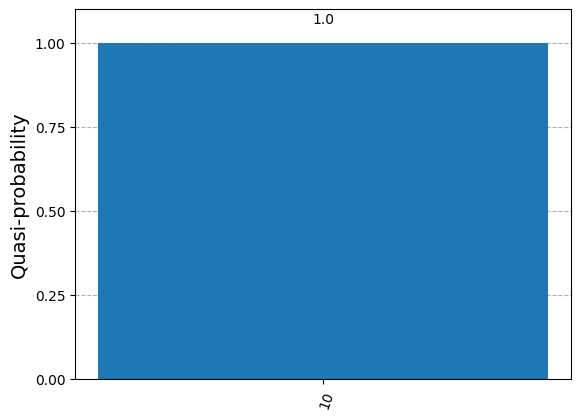
../../_images/f7cae45f92081d5f6f5c863f6d82945ebd35959615cb942b4f5564e9b9ac1c52.png

これを楽しむために、ランダムなビット発生器を新たな量子ビットとして追加し、 \(c\) と \(d\) をランダムに選び、超密度符号プロトコルを実行して、ビットが正しく送信されることを確認してみましょう。

rbg = QuantumRegister(1, "randomizer")
ebit0 = QuantumRegister(1, "A")
ebit1 = QuantumRegister(1, "B")

Alice_c = ClassicalRegister(1, "Alice c")
Alice_d = ClassicalRegister(1, "Alice d")

test = QuantumCircuit(rbg, ebit0, ebit1, Alice_d, Alice_c)

# Initialize the ebit
test.h(ebit0)
test.cx(ebit0, ebit1)
test.barrier()

# Use the 'randomizer' qubit twice to generate Alice's bits c and d.
test.h(rbg)
test.measure(rbg, Alice_c)
test.h(rbg)
test.measure(rbg, Alice_d)
test.barrier()

# Now the protocol runs, starting with Alice's actions, which depend
# on her bits.
with test.if_test((Alice_d, 1), label="Z"):
    test.z(ebit0)
with test.if_test((Alice_c, 1), label="X"):
    test.x(ebit0)
test.barrier()

# Bob's actions
test.cx(ebit0, ebit1)
test.h(ebit0)
test.barrier()

Bob_c = ClassicalRegister(1, "Bob c")
Bob_d = ClassicalRegister(1, "Bob d")
test.add_register(Bob_d)
test.add_register(Bob_c)
test.measure(ebit0, Bob_d)
test.measure(ebit1, Bob_c)

display(test.draw("mpl"))
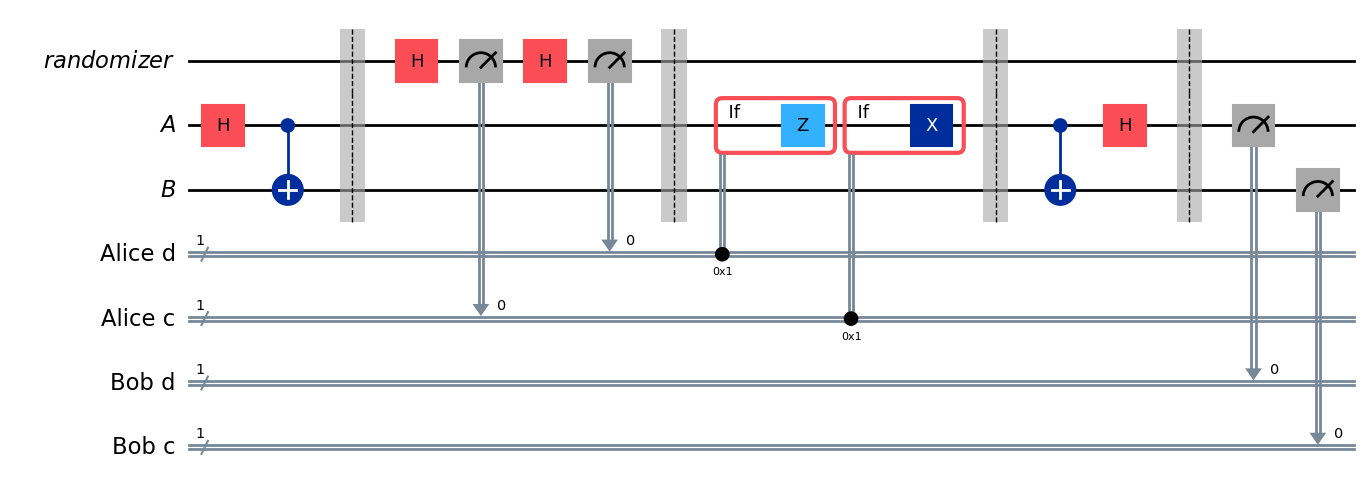
../../_images/b2b15094ea6f420aa676f4062407bb9a1df9d764d4fed77c4da099ffaa3f8df0.png

Aerシミュレーターを実行すると、結果が表示されます：アリスとボブの古典ビットは常に一致します。

result = AerSimulator().run(test).result()
statistics = result.get_counts()
display(plot_histogram(statistics))
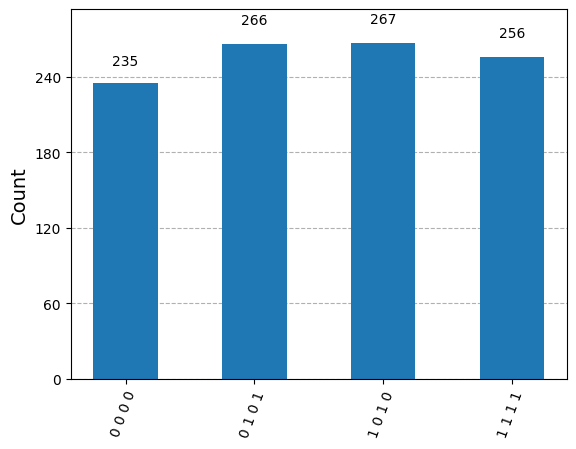
../../_images/72dd5c5e2ad8299a84cd5322149314f166fdbe1c8e69954357e80fb7dd335c51.png

3. CHSHゲーム#

この授業で最後に取り上げる例は、プロトコルではなく、 CHSHゲームと呼ばれる ゲームです。

この文脈でゲームというと、遊びやスポーツを目的としたものではなく、ゲーム理論的な意味での数学的に抽象化されたものを指します。ゲームの数学的な抽象化は、例えば経済学やコンピュータサイエンスで研究され、大きな実用性を持っています。

CHSHの文字は、この例が最初に記述された1969年の論文の著者、ジョン・クラウザー、マイケル・ホーン、アブナー・シモニー、リチャード・ホルトを指しています。彼らはこの例をゲームとしてではなく、実験として記述しています。しかし、ゲームとして説明することは、自然で直感的なことです。

CHSHゲームは、非局所ゲームと呼ばれるゲームのクラスに属するものです。非局所ゲームは、物理学、コンピュータサイエンス、数学と深い関わりを持ち、いまだ未解決の謎を抱えた魅力的なゲームです。ここでは、まず非局所ゲームとは何かを説明し、次にCHSHゲームに焦点を当て、その面白さを紹介します。

3.1 非局所ゲーム#

非局所ゲームとは、アリスとボブの2人のプレイヤーが特定の結果を得るために協力し合うゲームです。ゲームは審判によって運営され、審判はアリスとボブに知られた厳格なガイドラインに従って行動します。

アリスとボブはゲームの準備をすることはできますが、ゲームが始まるとコミュニケーションをとることは禁じられます。審判が刑事役で、アリスとボブが別室で尋問を受ける容疑者というように、ある種の安全な施設でゲームを行う設定が考えられます。別の想像で、アリスとボブは広大な距離を隔てており、ゲームの実行時間内では光の速度が許さないため通信が禁止されている、という設定もあります。つまり、アリスがボブにメッセージを送ろうとしても、ボブがそれを受け取るまでにゲームは終わってしまうし、その逆もまた然りです。

非局所ゲームの仕組みとして、まず審判がアリスとボブのそれぞれに質問をします。アリスの質問を \(x\) 、ボブの質問を \(y\) という文字で表すことにします。ここで、 \(x\) と \(y\) は古典的な状態であり、CHSHゲームでは \(x\) と \(y\) はビットであると考えます。

審判はランダム性を利用してこれらの問題を選択します。正確には、質問となるペア \((x,y)\) ごとに確率 \(p(x,y)\) が関連付けられており、審判はゲーム開始時に、この方法で問題を選択することを誓っています。アリスとボブを含む全員がこの確率を知っています。しかし、ゲームが始まるまで、どの組 \((x,y)\) が選ばれるかは誰も具体的に知りません。

アリスとボブは質問を受けたら、次に答えを出さなければなりません。アリスの答えは \(a\) 、ボブの答えは \(b\) です。繰り返しますが、これらは一般に古典状態であり、CHSH ゲームではビットです。

この時点で審判が判定を下します：アリスとボブは、ある固定されたルールに従って、一組の質問 \((x,y)\) に対して一組の答え \((a,b)\) が正しいとみなされるかどうかで、勝つか負けるかを決めます。ルールが異なればゲームも異なり、特にCHSHゲームのルールはこの後のセクションで具体的に説明されます。すでに述べられたように、ルールは誰にでも知られています。

次の図は、相互作用を図式化したものです。

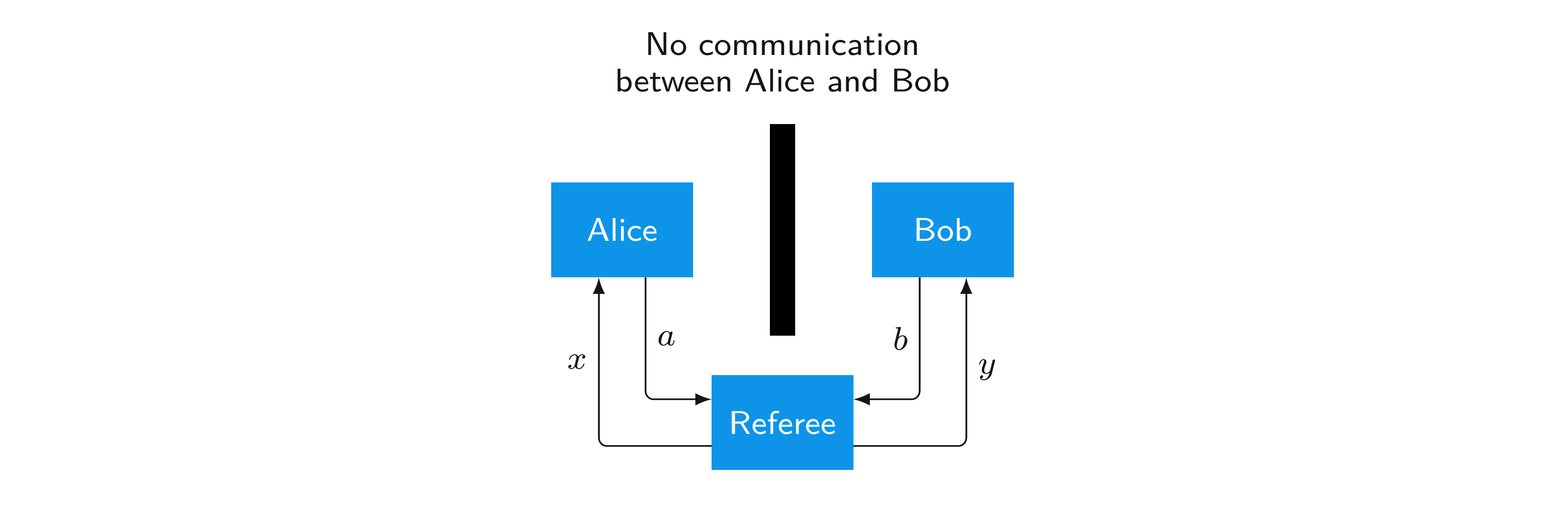
Nonlocal game

どの質問が聞かれるかわからないこと、特に各プレイヤーが他のプレイヤーの質問を知らないことが、アリスとボブにとって非局所ゲームを難しいものにしています。

審判の正確な説明は、非局所ゲームのインスタンスを定義します。これには、質問ペアの確率 \(p(x,y)\) の指定と、質問ペア \((x,y)\) に対して、答えのペア \((a,b)\) が勝つか負けるかを決定するルールが含まれます。

すぐにCHSHのゲームを見てみますが、他の非局所ゲームを考えてみるのも面白いです。非局所ゲームの中には、今日まで魅力的で謎に包まれているものもあれば、あまり面白くないものもあります。セットアップは単純ですが、複雑な作業が行われています。一部の非局所ゲームでは、アリスとボブの最適またはほぼ最適な戦略を計算することが非常に困難な場合があります。これは、非局所ゲームモデルの魅力的な性質の一部です。

3.2 CHSH ゲームの説明#

以下は CHSH ゲームの正確な説明です。ここで (上記のように) \(x\) はアリスの質問、 \(y\) はボブの質問、 \(a\) はアリスの返答、 \(b\) はボブの返答です。

  1. 質問と返答はすべてビットです: \(x,y,a,b\in\{0,1\}\)

  2. 審判は質問 \((x,y)\) を一様に無作為に選びます。つまり、 \((0,0)\) 、 \((0,1)\) 、 \((1,0)\) 、 \((1,1)\) の 4 つの可能性のそれぞれが、確率 \(1/4\) で選択されます。

  3. 返答 \((a,b)\) は、\(a\oplus b = x\wedge y\) の場合、質問 \((x,y)\) に対して勝ち、それ以外の場合は負けます。次の表は、 \((x,y)\) の質問のペアごとに、 \((a,b)\) の返答の勝敗条件をリスト化し、このルールを表しています。

\((x,y)\)

勝ち

負け

\((0,0)\)

\(a = b\)

\(a \not= b\)

\((0,1)\)

\(a = b\)

\(a \not= b\)

\((1,0)\)

\(a = b\)

\(a \not= b\)

\((1,1)\)

\(a \not= b\)

\(a = b\)

3.3 古典的戦略の限界#

では、CHSHゲームにおけるアリスとボブの戦略を、古典的戦略から考えてみましょう。

決定論的戦略#

ここではまず決定論的な戦略から始めます。アリスの返答 \(a\) は彼女が受ける質問 \(x\) の関数であり、同様にボブの返答 \(b\) は彼が受ける質問 \(y\) の関数です。したがって、例えば、質問が \(0\) のときのアリスの返答を \(a(0)\) 、質問が \(1\) のときのアリスの返答を \(a(1)\) と書くことができます。

どの決定論的戦略も、CHSHゲームに毎回勝つことはできません。このことを説明する1つの方法は、可能な決定論的戦略を1つ1つ調べ、そのどれもが4つの質問ペアのうち少なくとも1つに対して負けることをチェックすることです。アリスとボブはそれぞれ1ビットから1ビットまでの4つの関数 (レッスン 1 で遭遇した) から選ぶことができるので、チェックすべき決定論的戦略は全部で \(16\) 種類になります。

この事実を分析的に推論することもできます。アリスとボブの戦略が \((x,y) = (0,0)\) のときに勝った場合、それは \(a(0) = b(0)\) でなければなりません。彼らの戦略が \((x,y) = (0,1)\) で勝った場合、 \(a(0) = b(1)\) と結論付けられます。同様に、戦略が \((x,y)=(1,0)\) で勝った場合、 \(a(1) = b(0)\) になります。 したがって、彼らの戦略が 3 つの可能性すべてで勝った場合、次のようになります。

\[ b(1) = a(0) = b(0) = a(1). \]

これは、最後のケース \((x,y) = (1,1)\) でこの戦略が負けることを意味します。勝つには、 \(a(1) \not= b(1)\) が必要だからです。

したがって、毎回勝つ決定論的な戦略はあり得ません。4つのケースのうち3つのケース ( \(a(0)=a(1)=b(0)=b(1)=0\) など) で勝つ戦略とするのが非常に素直であり、アリスとボブが決定論的戦略を使用して勝つのは最大の確率は \(3/4\) です。

確率的戦略#

今、結論を出したように、アリスとボブは決定論的戦略を用いてCHSHゲームに75％の確率で勝利する以上のことはできないのです。しかし、確率的な戦略ではどうでしょうか。ランダム性を利用することは、アリスとボブのランダムな選択に相関があるような共有ランダム性の可能性も含めて、アリスとボブを助けることができるでしょうか？

確率論的戦略は、アリスとボブが勝つ確率を高めるのに全く役立たないことが分かります。これは、すべての確率的戦略が、決定論的戦略のランダムな選択と見なすことができるからです。（最初の授業で述べたように）確率的演算が決定論的演算のランダムな選択と見なすことができるのと同じです。平均値が最大値より大きくなることはないので、確率的戦略は全体的な勝率の点では何の利点もないことになります。

したがって、確率 \(3/4\) で勝つことは、決定論的であれ確率論的であれ、あらゆる古典的戦略を用いてアリスとボブができるベストな確率です。

3.4 CHSH ゲームの戦略#

ここで、アリスとボブが、量子的な戦略を用いることで、より良い結果を得ることができるのだろうか、という自然な疑問が生じます。特に、次の図のように、エンタングルした量子状態をゲームをする前に共有した場合、勝率を上げることができるでしょうか？

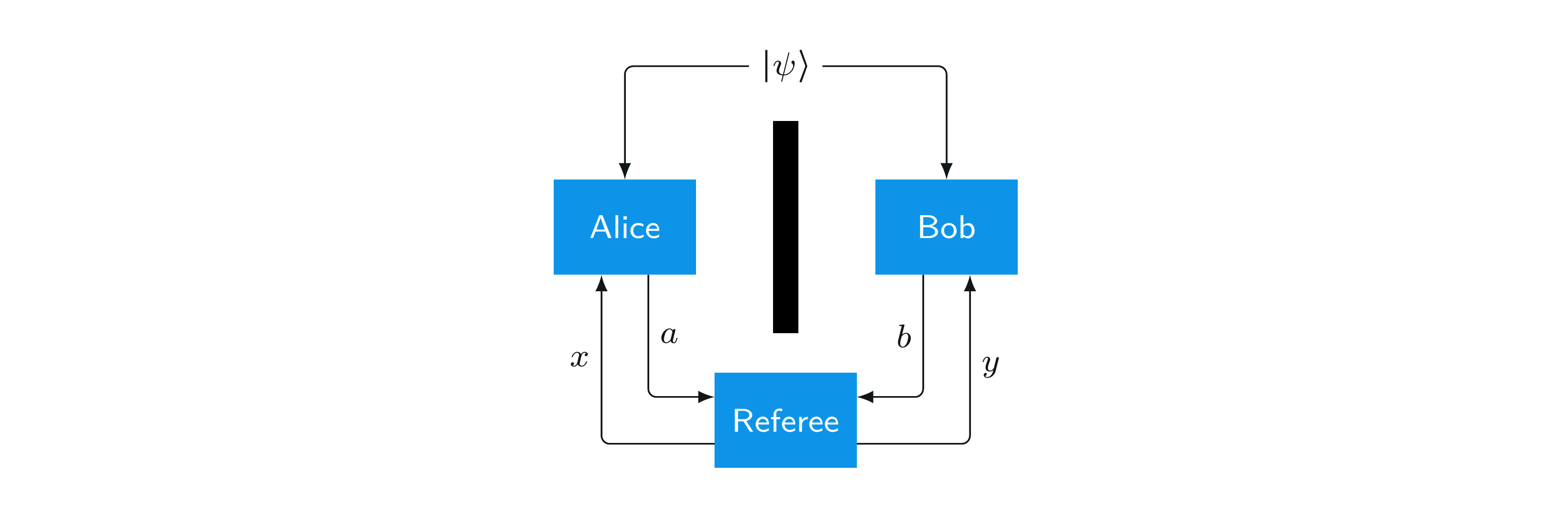
Nonlocal game with entanglement

答えは「イエス」であり、これがこの例の最大のポイントであり、なぜこれが面白いのか、という点です。では、エンタングルメントを使って、アリスとボブがこのゲームでどのようにうまくやれるか、具体的に見ていきましょう。

必要なベクトルと行列#

まず、各実数 \(\theta\) （ラジアン単位で測った角度）に対して、量子ビットの状態ベクトル \(\vert \psi_{\theta}\rangle\) を以下のように定義します。

\[ \vert\psi_{\theta}\rangle = \cos(\theta)\vert 0\rangle + \sin(\theta) \vert 1\rangle \]

簡単な例を紹介します：

\[\begin{split} \begin{aligned} \vert\psi_{0}\rangle & = \vert 0\rangle \\ \vert\psi_{\pi/2}\rangle & = \vert 1\rangle \\ \vert\psi_{\pi/4}\rangle & = \vert + \rangle \\ \vert\psi_{-\pi/4}\rangle & = \vert - \rangle \end{aligned} \end{split}\]

また、以下のような例もあり、解析すると以下のようになります：

\[\begin{split} \begin{aligned} \vert\psi_{-\pi/8}\rangle & = \frac{\sqrt{2 + \sqrt{2}}}{2}\vert 0\rangle -\frac{\sqrt{2 - \sqrt{2}}}{2}\vert 1\rangle \\ \vert\psi_{\pi/8}\rangle & = \frac{\sqrt{2 + \sqrt{2}}}{2}\vert 0\rangle + \frac{\sqrt{2 - \sqrt{2}}}{2}\vert 1\rangle \\ \vert\psi_{3\pi/8}\rangle & = \frac{\sqrt{2 - \sqrt{2}}}{2}\vert 0\rangle -\frac{\sqrt{2 + \sqrt{2}}}{2}\vert 1\rangle \\ \vert\psi_{5\pi/8}\rangle & = -\frac{\sqrt{2 - \sqrt{2}}}{2}\vert 0\rangle + \frac{\sqrt{2 + \sqrt{2}}}{2}\vert 1\rangle \\ \end{aligned} \end{split}\]

一般的な形を見ると、これらのベクトルのうち任意の2つのベクトル間の内積は次のような式になることがわかります：

\[ \langle \psi_{\alpha} \vert \psi_{\beta} \rangle = \cos(\alpha)\cos(\beta) + \sin(\alpha)\sin(\beta) = \cos(\alpha-\beta). \tag{3} \]

具体的に見ると、これらのベクトルには実数の項目しかないので、複素共役の心配はありません。内積は、余弦の積に正弦の積を加えたものです。そこで、いわゆる加法定理を使って簡略化することができます。この式は、実数の単位ベクトル間の内積を、それらの間の角度の余弦として幾何学的に解釈することを明らかにしています。

さて、これらのベクトルのうち任意の2つのテンソル積と \(\vert \phi^+\rangle\) 状態との内積を計算すると、分母に \(\sqrt{2}\) が入ることを除いて、同様の式が得られます：

\[ \langle \psi_{\alpha} \otimes \psi_{\beta} \vert \phi^+ \rangle = \frac{\cos(\alpha)\cos(\beta) + \sin(\alpha)\sin(\beta)}{\sqrt{2}} = \frac{\cos(\alpha-\beta)}{\sqrt{2}}. \tag{4} \]

この特定の内積に興味がある理由は、まもなく明らかになりますが、今は単に数式として見ているだけです。

次に、角度 \(\theta\) ごとにユニタリー行列 \(U_{\theta}\) を次のように定義します。

\[ U_{\theta} = \vert 0 \rangle \langle \psi_{\theta} \vert + \vert 1\rangle\langle \psi_{\theta+\pi/2} \vert \]

直観的に言えば、演算として、この行列は \(\vert\psi_{\theta}\rangle\) を \(\vert 0\rangle\) に、 \(\vert \psi_{\theta + \pi/2}\rangle\) を \(\vert 1\rangle\) にマッピングします。これがユニタリー行列であることを確認するために重要なことは、ベクトル \(\vert\psi_{\theta}\rangle\) と \(\vert\psi_{\theta + \pi/2}\rangle\) がすべての角度 \(\theta\) に対して直交することです：

\[ \langle \psi_{\theta} \vert \psi_{\theta + \pi/2} \rangle = \cos(\pi/2) = 0. \]

したがって、以下のようになります。

\[\begin{split} \begin{aligned} U_{\theta} U_{\theta}^{\dagger} & = \bigl(\vert 0 \rangle \langle \psi_{\theta} \vert + \vert 1\rangle\langle \psi_{\theta+\pi/2} \vert\bigr) \bigl(\vert \psi_{\theta} \rangle \langle 0 \vert + \vert \psi_{\theta+\pi/2}\rangle\langle 1 \vert\bigr) \\ & = \vert 0 \rangle \langle \psi_{\theta} \vert \psi_{\theta} \rangle \langle 0 \vert + \vert 0 \rangle \langle \psi_{\theta} \vert \psi_{\theta+\pi/2} \rangle \langle 1 \vert + \vert 1 \rangle \langle \psi_{\theta+\pi/2} \vert \psi_{\theta} \rangle \langle 0 \vert + \vert 1 \rangle \langle \psi_{\theta+\pi/2} \vert \psi_{\theta+\pi/2} \rangle \langle 1 \vert \\ & = \vert 0 \rangle \langle 0 \vert + \vert 1 \rangle \langle 1 \vert\\ & = \mathbb{1}. \end{aligned} \end{split}\]

別の方法として、この行列を次のように明示的に書くこともできます。

\[\begin{split} U_{\theta} = \begin{pmatrix} \cos(\theta) & \sin(\theta)\\ \cos(\theta+ \pi/2) & \sin(\theta + \pi/2) \end{pmatrix} = \begin{pmatrix} \cos(\theta) & \sin(\theta)\\ -\sin(\theta) & \cos(\theta) \end{pmatrix}. \end{split}\]

これは回転行列の例で、具体的には実数の要素を持つ2次元ベクトルを原点を中心に \(-\theta\) の角度で回転させます。さまざまな式の回転の名前付けとパラメーター化の標準的な規則に従うと、以下のような \(U_{\theta} = R_y(-2\theta)\) が得られます。

\[\begin{split} R_y(\theta) = \begin{pmatrix} \cos(\theta/2) & -\sin(\theta/2)\\ \sin(\theta/2) & \cos(\theta/2) \end{pmatrix}. \end{split}\]

戦略の説明#

これで、量子的な戦略について説明できます。

  • アリスとボブは、eビットを共有してゲームを開始します: アリスは量子ビット \(\mathsf{A}\) を保持し、ボブは量子ビット \(\mathsf{B}\) を保持し、 \(\vert\psi^+\rangle\) 状態にある2つの量子ビット \((\mathsf{X},\mathsf{Y})\) を共に持ちます。

  • アリスの動作は次のとおりです：

    • 彼女の質問が \(x=0\) の場合、彼女は \(U_{0}\) を量子ビット \(\mathsf{A}\) に適用します。

    • 彼女の質問が \(x=1\) の場合、彼女は \(U_{\pi/4}\) を量子ビット \(\mathsf{A}\) に適用します。

アリスが \(\mathsf{A}\) に対して実行する演算は、代わりに次のように記述できます：

\[\begin{split} \begin{cases} U_0 & \text{if x = 0}\\ U_{\pi/4} & \text{if x = 1} \end{cases} \end{split}\]

この演算を適用した後、彼女は \(\mathsf{A}\) を標準基底で測定し、測定結果を返答 \(a\) に設定します。

  • ボブの動作は次のとおりです：

    • 彼の質問が \(y=0\) の場合、彼は \(U_{\pi/8}\) を量子ビット \(\mathsf{B}\) に適用します。

    • 彼の質問が \(y=1\) の場合、彼は \(U_{-\pi/8}\) を量子ビット \(\mathsf{B}\) に適用します。

アリスの場合と同様に、\(\mathsf{B}\) に対するボブの演算を次のように記述できます：

\[\begin{split} \begin{cases} U_{\pi/8} & \text{if y = 0}\\ U_{-\pi/8} & \text{if y = 1} \end{cases} \end{split}\]

この演算を適用した後、標準基底で \(\mathsf{B}\) を測定し、測定結果を返答 \(b\) に設定します。

この戦略の量子回路図を次に示します：

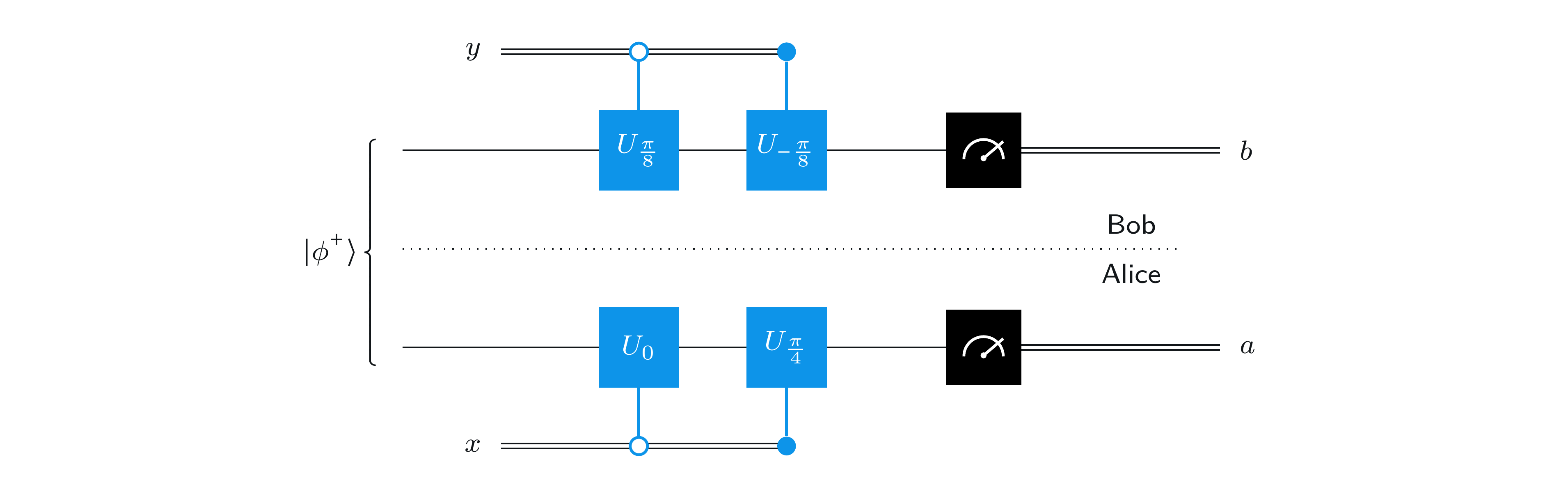
CHSH game circuit

この図には、2つの一般の制御ゲートがあります。1つは上にある \(U_{-\pi/8}\) のもので、もう1つは下にある \(U_{\pi/4}\) のものです。 また、制御ゲートのような別のゲートも2つあります。上側の \(U_{\pi/8}\) のものと、下側の \(U_{0}\) のものですが、制御を表す丸が塗りつぶされていません。このゲートは、制御ビットが \(0\) の場合に実行されます (通常の制御ゲートのように \(1\) の場合に実行されるのではなく)。したがって、ボブは、 \(y=0\) の場合は自分の量子ビットに \(U_{\pi/8}\) を実行し、 \(y=1\) の場合は \(U_{-\pi/8}\) を実行します。アリスは、 \(x=0\) の場合に自分の量子ビットに \(U_0\) を実行し、 \(x=1\) の場合は \(U_{\pi/4}\) を実行します。以上の動きは、上記のプロトコルの説明と一致しています。

アリスとボブに対するこの戦略がどの程度うまく機能するかは、まだ解明されていません。これを行うために、4種類の質問のペアを個別に調べてみることにします。

ケースバイケース分析#

(0,0)#

ケース 1: \((x,y) = (0,0)\) の場合

この場合、アリスは自分の量子ビットで \(U_{0}\) を実行し、ボブは自分の量子ビットで \(U_{\pi/8}\) を実行するため、彼らが演算を実行した後は、2つの量子ビット \((\mathsf{A},\mathsf{B})\) の状態は、次のようになります。

\[\begin{split} \begin{aligned} \bigl(U_0 \otimes U_{\pi/8}\bigr) \vert \phi^+\rangle & = \vert 00 \rangle \langle \psi_0 \otimes \psi_{\pi/8}\vert \phi^+\rangle + \vert 01 \rangle \langle \psi_0 \otimes\psi_{5\pi/8}\vert \phi^+\rangle \\ & \qquad + \vert 10 \rangle \langle \psi_{\pi/2} \otimes \psi_{\pi/8}\vert \phi^+\rangle + \vert 11 \rangle \langle \psi_{\pi/2} \otimes \psi_{5\pi/8}\vert \phi^+\rangle\\[1mm] & = \frac{ \cos\bigl(-\frac{\pi}{8}\bigr) \vert 00\rangle + \cos\bigl(-\frac{5\pi}{8}\bigr) \vert 01\rangle + \cos\bigl(\frac{3\pi}{8}\bigr) \vert 10\rangle + \cos\bigl(-\frac{\pi}{8}\bigr) \vert 11\rangle}{\sqrt{2}}. \end{aligned} \end{split}\]

したがって、4つの返答のペア \((a,b)\) の確率は次のようになります。

\[\begin{split} \begin{aligned} \operatorname{Pr}\bigl((a,b)=(0,0)\bigr) & = \frac{1}{2}\cos^2\Bigl(-\frac{\pi}{8}\Bigr) = \frac{2+\sqrt{2}}{8} \\ \operatorname{Pr}\bigl((a,b)=(0,1)\bigr) & = \frac{1}{2}\cos^2\Bigl(-\frac{5\pi}{8}\Bigr) = \frac{2-\sqrt{2}}{8}\\ \operatorname{Pr}\bigl((a,b)=(1,0)\bigr) & = \frac{1}{2}\cos^2\Bigl(\frac{3\pi}{8}\Bigr) = \frac{2-\sqrt{2}}{8}\\ \operatorname{Pr}\bigl((a,b)=(1,1)\bigr) & = \frac{1}{2}\cos^2\Bigl(-\frac{\pi}{8}\Bigr) = \frac{2+\sqrt{2}}{8} \end{aligned} \end{split}\]

このとき、 \(a=b\) と \(a\not=b\) の確率は、適当な和をとることで得られます：

\[\begin{split} \begin{aligned} \operatorname{Pr}(a = b) & = \frac{2 + \sqrt{2}}{4}\\ \operatorname{Pr}(a \not= b) & = \frac{2 - \sqrt{2}}{4} \end{aligned} \end{split}\]

質問のペア \((0,0)\) に対して、アリスとボブは \(a=b\) のときに勝つので、この場合、勝つ確率は、以下です。

\[ \frac{2 + \sqrt{2}}{4}. \]

(0, 1)#

ケース 2: \((x,y) = (0,1)\) の場合

この場合、アリスは自分の量子ビットで \(U_{0}\) を実行し、ボブは自分の量子ビットで \(U_{-\pi/8}\) を実行するため、彼らが演算を実行した後は、2つの量子ビット \((\mathsf{A},\mathsf{B})\) の状態は、次のようになります。

\[\begin{split} \begin{aligned} \bigl(U_0 \otimes U_{-\pi/8}\bigr) \vert \phi^+\rangle & = \vert 00 \rangle \langle \psi_0 \otimes \psi_{-\pi/8}\vert \phi^+\rangle + \vert 01 \rangle \langle \psi_0 \otimes\psi_{3\pi/8}\vert \phi^+\rangle \\ & \qquad + \vert 10 \rangle \langle \psi_{\pi/2} \otimes \psi_{-\pi/8}\vert \phi^+\rangle + \vert 11 \rangle \langle \psi_{\pi/2} \otimes \psi_{3\pi/8}\vert \phi^+\rangle\\[1mm] & = \frac{ \cos\bigl(\frac{\pi}{8}\bigr) \vert 00\rangle + \cos\bigl(-\frac{3\pi}{8}\bigr) \vert 01\rangle + \cos\bigl(\frac{5\pi}{8}\bigr) \vert 10\rangle + \cos\bigl(\frac{\pi}{8}\bigr) \vert 11\rangle}{\sqrt{2}}. \end{aligned} \end{split}\]

したがって、4つの返答のペア \((a,b)\) の確率は次のようになります。

\[\begin{split} \begin{aligned} \operatorname{Pr}\bigl((a,b)=(0,0)\bigr) & = \frac{1}{2}\cos^2\Bigl(\frac{\pi}{8}\Bigr) = \frac{2+\sqrt{2}}{8} \\ \operatorname{Pr}\bigl((a,b)=(0,1)\bigr) & = \frac{1}{2}\cos^2\Bigl(-\frac{3\pi}{8}\Bigr) = \frac{2-\sqrt{2}}{8}\\ \operatorname{Pr}\bigl((a,b)=(1,0)\bigr) & = \frac{1}{2}\cos^2\Bigl(\frac{5\pi}{8}\Bigr) = \frac{2-\sqrt{2}}{8}\\ \operatorname{Pr}\bigl((a,b)=(1,1)\bigr) & = \frac{1}{2}\cos^2\Bigl(\frac{\pi}{8}\Bigr) = \frac{2+\sqrt{2}}{8} \end{aligned} \end{split}\]

前回と同じように、 \(a=b\) と \(a\not=b\) の確率は、適当な和をとることで得られます：

\[\begin{split} \begin{aligned} \operatorname{Pr}(a = b) & = \frac{2 + \sqrt{2}}{4}\\ \operatorname{Pr}(a \not= b) & = \frac{2 - \sqrt{2}}{4} \end{aligned} \end{split}\]

質問のペア \((0,1)\) に対して、アリスとボブは \(a=b\) のときに勝つので、この場合、勝つ確率は、以下です。

\[ \frac{2 + \sqrt{2}}{4}. \]

(1, 0)#

ケース 3: \((x,y) = (1,0)\) の場合

この場合、アリスは自分の量子ビットで \(U_{\pi/4}\) を実行し、ボブは自分の量子ビットで \(U_{-\pi/8}\) を実行するため、彼らが演算を実行した後は、2つの量子ビット \((\mathsf{A},\mathsf{B})\) の状態は、次のようになります。

\[\begin{split} \begin{aligned} \bigl(U_{\pi/4} \otimes U_{\pi/8}\bigr) \vert \phi^+\rangle & = \vert 00 \rangle \langle \psi_{\pi/4} \otimes \psi_{\pi/8}\vert \phi^+\rangle + \vert 01 \rangle \langle \psi_{\pi/4} \otimes\psi_{5\pi/8}\vert \phi^+\rangle \\ & \qquad + \vert 10 \rangle \langle \psi_{3\pi/4} \otimes \psi_{\pi/8}\vert \phi^+\rangle + \vert 11 \rangle \langle \psi_{3\pi/4} \otimes \psi_{5\pi/8}\vert \phi^+\rangle\\[1mm] & = \frac{ \cos\bigl(\frac{\pi}{8}\bigr) \vert 00\rangle + \cos\bigl(-\frac{3\pi}{8}\bigr) \vert 01\rangle + \cos\bigl(\frac{5\pi}{8}\bigr) \vert 10\rangle + \cos\bigl(\frac{\pi}{8}\bigr) \vert 11\rangle}{\sqrt{2}}. \end{aligned} \end{split}\]

したがって、4つの返答のペア \((a,b)\) の確率は次のようになります。

\[\begin{split} \begin{aligned} \operatorname{Pr}\bigl((a,b)=(0,0)\bigr) & = \frac{1}{2}\cos^2\Bigl(\frac{\pi}{8}\Bigr) = \frac{2+\sqrt{2}}{8} \\ \operatorname{Pr}\bigl((a,b)=(0,1)\bigr) & = \frac{1}{2}\cos^2\Bigl(-\frac{3\pi}{8}\Bigr) = \frac{2-\sqrt{2}}{8}\\ \operatorname{Pr}\bigl((a,b)=(1,0)\bigr) & = \frac{1}{2}\cos^2\Bigl(\frac{5\pi}{8}\Bigr) = \frac{2-\sqrt{2}}{8}\\ \operatorname{Pr}\bigl((a,b)=(1,1)\bigr) & = \frac{1}{2}\cos^2\Bigl(\frac{\pi}{8}\Bigr) = \frac{2+\sqrt{2}}{8} \end{aligned} \end{split}\]

前回と同じように、 \(a=b\) と \(a\not=b\) の確率は、適当な和をとることで得られます：

\[\begin{split} \begin{aligned} \operatorname{Pr}(a = b) & = \frac{2 + \sqrt{2}}{4}\\ \operatorname{Pr}(a \not= b) & = \frac{2 - \sqrt{2}}{4} \end{aligned} \end{split}\]

質問のペア \((1,0)\) に対して、アリスとボブは \(a=b\) のときに勝つので、この場合、勝つ確率は、以下です。

\[ \frac{2 + \sqrt{2}}{4}. \]

(1, 1)#

ケース 4: \((x,y) = (1,1)\) の場合

最後のケースは、この場合、勝利条件が異なるので、予想通り、ちょっと違います。 \(x\) と \(y\) がともに \(1\) のとき、 \(a\) と \(b\) が異なるとき、アリスとボブは勝利します。この場合、アリスは自分の量子ビットに \(U_{\pi/4}\) を、ボブは自分の量子ビットに \(U_{-\pi/8}\) の演算を行うので、彼らが演算を実行した後は、2つの量子ビット \((\mathsf{A},\mathsf{B})\) の状態は、次のようになります。

\[\begin{split} \begin{aligned} \bigl(U_{\pi/4} \otimes U_{-\pi/8}\bigr) \vert \phi^+\rangle & = \vert 00 \rangle \langle \psi_{\pi/4} \otimes \psi_{-\pi/8}\vert \phi^+\rangle + \vert 01 \rangle \langle \psi_{\pi/4} \otimes\psi_{3\pi/8}\vert \phi^+\rangle \\ & \qquad + \vert 10 \rangle \langle \psi_{3\pi/4} \otimes \psi_{-\pi/8}\vert \phi^+\rangle + \vert 11 \rangle \langle \psi_{3\pi/4} \otimes \psi_{3\pi/8}\vert \phi^+\rangle\\[1mm] & = \frac{ \cos\bigl(\frac{3\pi}{8}\bigr) \vert 00\rangle + \cos\bigl(-\frac{\pi}{8}\bigr) \vert 01\rangle + \cos\bigl(\frac{7\pi}{8}\bigr) \vert 10\rangle + \cos\bigl(\frac{3\pi}{8}\bigr) \vert 11\rangle}{\sqrt{2}}. \end{aligned} \end{split}\]

したがって、4つの返答のペア \((a,b)\) の確率は次のようになります。

\[\begin{split} \begin{aligned} \operatorname{Pr}\bigl((a,b)=(0,0)\bigr) & = \frac{1}{2}\cos^2\Bigl(\frac{3\pi}{8}\Bigr) = \frac{2-\sqrt{2}}{8} \\ \operatorname{Pr}\bigl((a,b)=(0,1)\bigr) & = \frac{1}{2}\cos^2\Bigl(-\frac{\pi}{8}\Bigr) = \frac{2+\sqrt{2}}{8}\\ \operatorname{Pr}\bigl((a,b)=(1,0)\bigr) & = \frac{1}{2}\cos^2\Bigl(\frac{7\pi}{8}\Bigr) = \frac{2+\sqrt{2}}{8}\\ \operatorname{Pr}\bigl((a,b)=(1,1)\bigr) & = \frac{1}{2}\cos^2\Bigl(\frac{3\pi}{8}\Bigr) = \frac{2-\sqrt{2}}{8} \end{aligned} \end{split}\]

この他の3つのケースと確率が事実上入れ替わっています。 \(a=b\) と \(a\not=b\) の確率は、合計することで得られます。

\[\begin{split} \begin{aligned} \operatorname{Pr}(a = b) & = \frac{2 - \sqrt{2}}{4}\\ \operatorname{Pr}(a \not= b) & = \frac{2 + \sqrt{2}}{4} \end{aligned} \end{split}\]

質問のペア \((1,1)\) に対して、アリスとボブは \(a\not=b\) のときに勝つので、この場合、勝つ確率は、以下です。

\[ \frac{2 + \sqrt{2}}{4}. \]

どのケースでも同じ確率で勝ちます。

\[ \frac{2 + \sqrt{2}}{4} \approx 0.85. \]

したがって、これが全体として勝利する確率となります。これは、古典的な戦略よりもはるかに優れています；古典的な戦略の勝利確率の上限は \(3/4\) でした。これは非常に興味深い例です。

この確率は、量子的な戦略にとって最適な勝率であり、どんなエンタングル状態や測定法を選んでも、これ以上の勝率は得られないのです。この事実はツィレルソンの不等式と呼ばれ、最初にこれを証明したボリス・ツィレルソンにちなんで名づけられたものです。ツィレルソンは、CHSH実験をゲームとして最初に説明した人物でもあります。

幾何学的描像#

上記の戦略を幾何学的に考えることが可能であり、アリスとボブの演算に選ばれた様々な角度の関係を理解するのに役立つかもしれません。

アリスが実際に行うことは、質問 \(x\) によって角度 \(\alpha\) を選び、 \(U_{\alpha}\) を自分の量子ビットに適用して測定することです。同様に、ボブは \(y\) によって角度 \(\beta\) を選び、 \(U_{\beta}\) を自分の量子ビットに適用して測定します。 \(\alpha\) と \(\beta\) は以下のように選びました。

\[\begin{split} \begin{aligned} \alpha & = \begin{cases} 0 & x=0\\ \pi/4 & x=1 \end{cases}\\[2mm] \beta & = \begin{cases} \pi/8 & y = 0\\ -\pi/8 & y = 1. \end{cases} \end{aligned} \end{split}\]

しかし、とりあえず、 \(\alpha\) と \(\beta\) は任意とします。アリスは \(\alpha\) を選ぶことで、事実上次のようなベクトルの正規直交基底を定義しています：

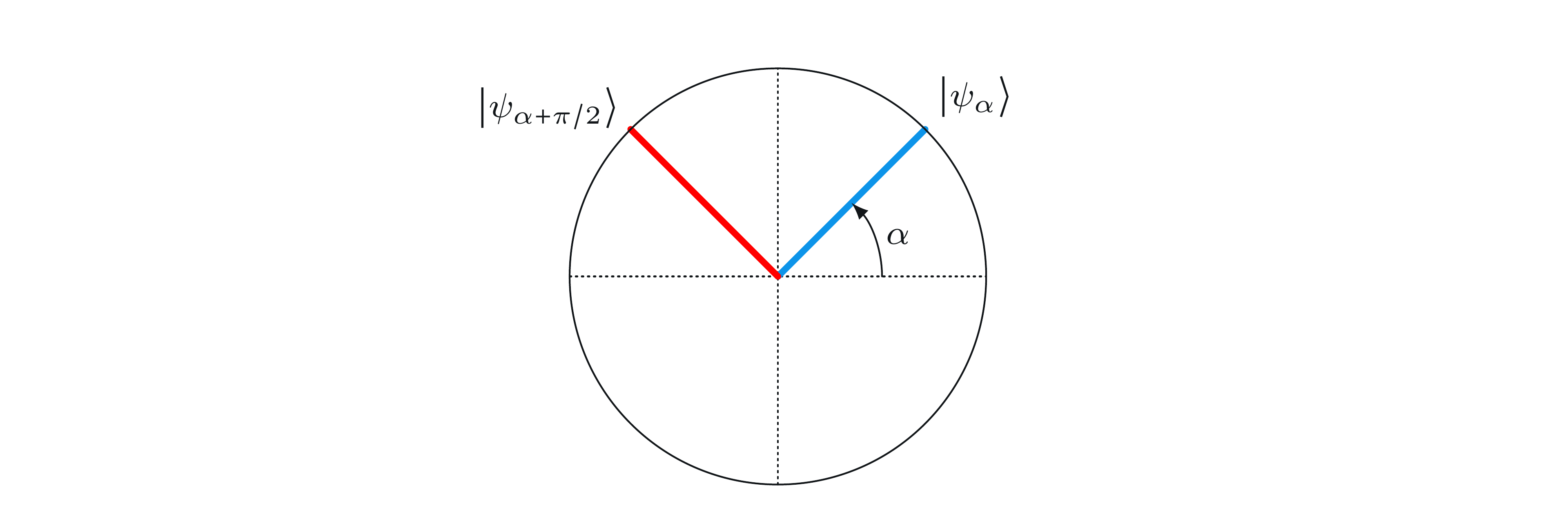
Basis for Alice

ボブも同様ですが、彼の角度は \(\beta\) です:

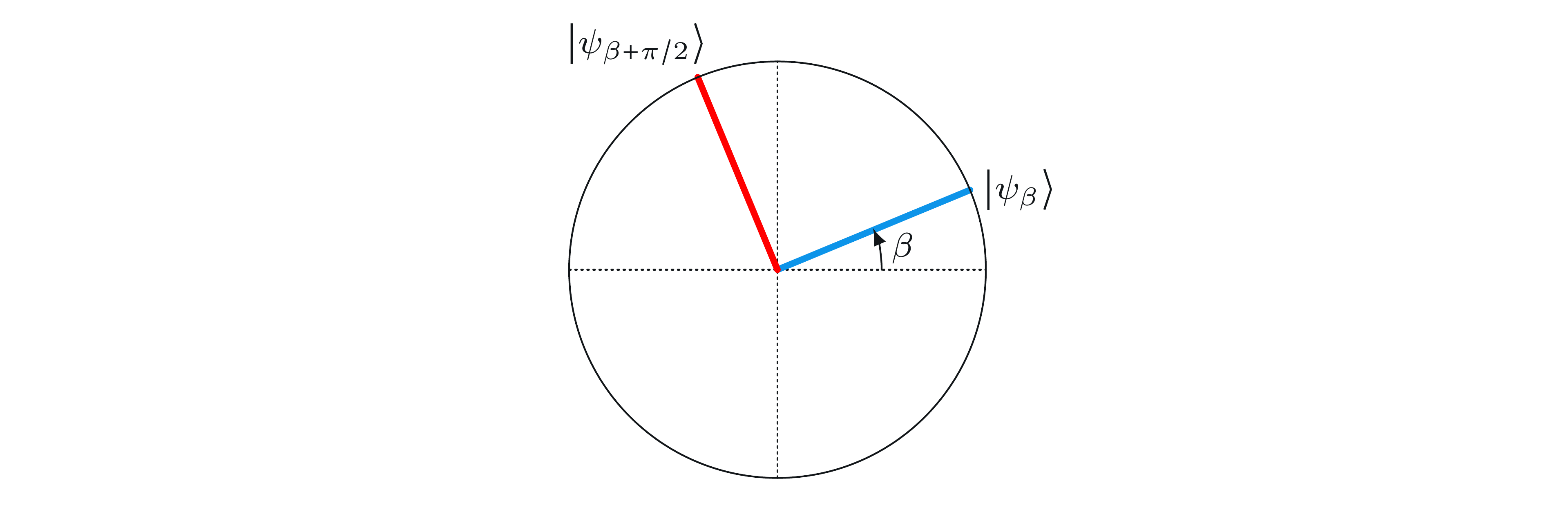
Basis for Bob

ベクトルの色はアリスとボブの答えに対応しており、青が \(0\) 、赤が \(1\) です。

さて、( \(3\) )と( \(4\) )を組み合わせると、次のような式になります。

\[ \langle \psi_{\alpha} \otimes\psi_{\beta} \vert \phi^+ \rangle = \frac{1}{\sqrt{2}} \langle \psi_{\alpha} \vert \psi_{\beta} \rangle; \]

これは、すべての実数 \(\alpha\) と \(\beta\) に当てはまります。

\(\alpha\) と \(\beta\) を変数として、上記と同じ類の分析に従うと、次のことがわかります：

\[\begin{split} \begin{aligned} & \bigl(U_{\alpha} \otimes U_{\beta}\bigr) \vert \phi^+\rangle\\ & \qquad = \vert 00 \rangle \langle \psi_{\alpha} \otimes \psi_{\beta}\vert \phi^+\rangle + \vert 01 \rangle \langle \psi_{\alpha} \otimes\psi_{\beta + \pi/2}\vert \phi^+\rangle \\ & \qquad \qquad + \vert 10 \rangle \langle \psi_{\alpha+\pi/2} \otimes \psi_{\beta}\vert \phi^+\rangle + \vert 11 \rangle \langle \psi_{\alpha+\pi/2} \otimes \psi_{\beta+\pi/2}\vert \phi^+\rangle\\[1mm] & \qquad = \frac{ \langle \psi_\alpha \vert \psi_\beta \rangle \vert 00\rangle + \langle \psi_\alpha \vert \psi_{\beta+\pi/2} \rangle \vert 01\rangle + \langle \psi_{\alpha+\pi/2} \vert \psi_\beta \rangle \vert 10\rangle + \langle \psi_{\alpha+\pi/2} \vert \psi_{\beta+\pi/2} \rangle \vert 11\rangle }{\sqrt{2}}. \end{aligned} \end{split}\]

そして、次の2つの公式が結論づけられます：

\[\begin{split} \begin{aligned} \operatorname{Pr}(a = b) & = \frac{1}{2} \vert \langle \psi_\alpha \vert \psi_\beta \rangle \vert^2 + \frac{1}{2} \vert \langle \psi_{\alpha+\pi/2} \vert \psi_{\beta+\pi/2} \rangle \vert^2 = \cos^2(\alpha - \beta)\\[2mm] \operatorname{Pr}(a \not= b) & = \frac{1}{2} \vert \langle \psi_\alpha \vert \psi_{\beta+\pi/2} \rangle \vert^2 + \frac{1}{2} \vert \langle \psi_{\alpha+\pi/2} \vert \psi_\beta \rangle \vert^2 = \sin^2(\alpha - \beta). \end{aligned} \end{split}\]

アリスとボブが選んだ基底を重ね合わせることをイメージすれば、この式と上の図を結びつけることができます。

戦略を探る#

(0, 0)#

\((x,y) = (0,0)\) のとき、アリスとボブは \(\alpha = 0\) と \(\beta = \pi/8\) を選び、それらの基底を重ね合わせることで、次の図が得られます：

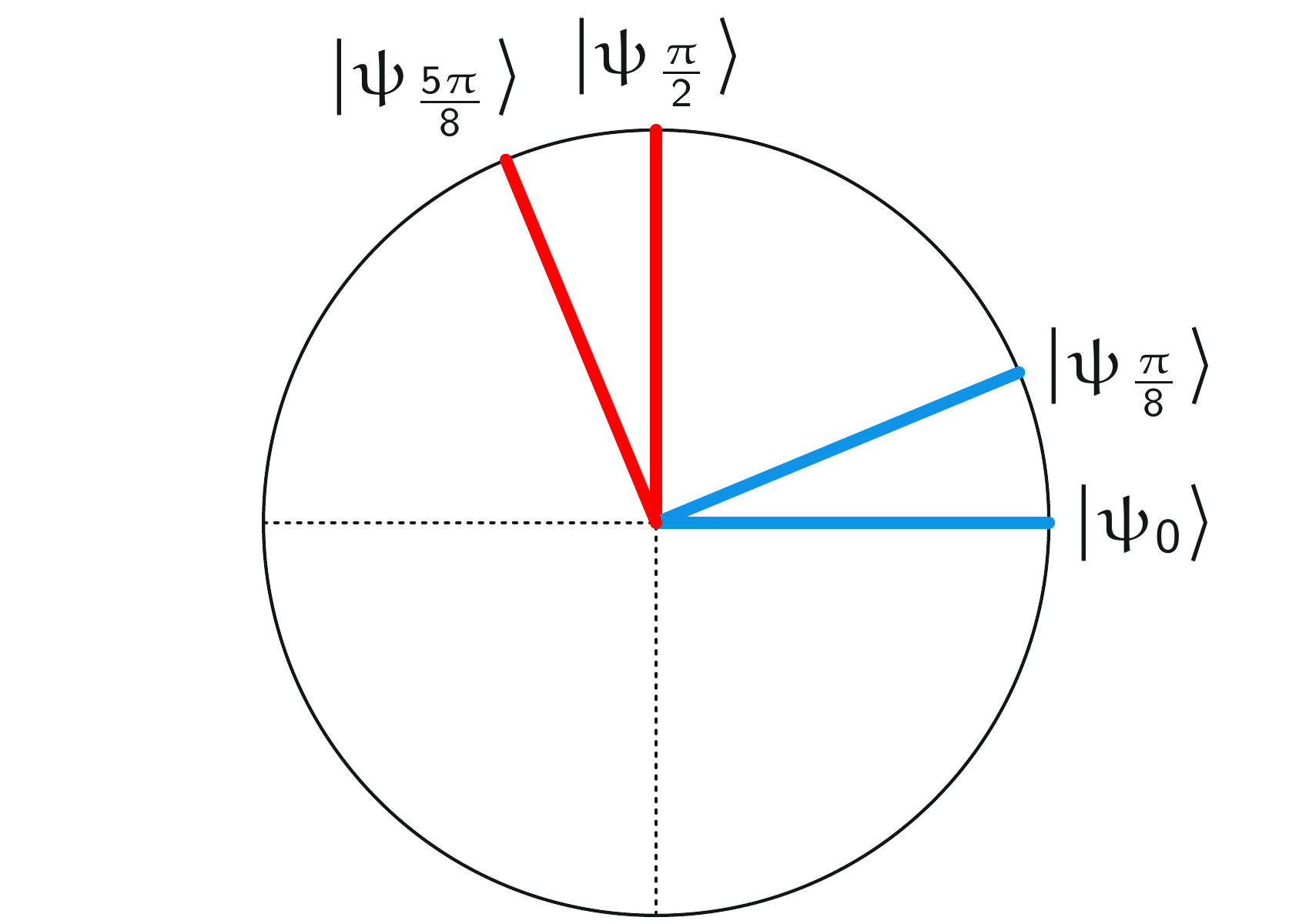
Alice and Bob bases case 1

赤いベクトルの間の角度は \(\pi/8\) であり、これは2つの青いベクトルの間の角度と同じです。アリスとボブの結果が一致する確率は、この角度の余弦二乗です。

\[ \cos^2\Bigl(\frac{\pi}{8}\Bigr) = \frac{2 + \sqrt{2}}{4}, \]

一方、返答が一致しない確率はこの角度の正弦二乗です。

\[ \sin^2\Bigl(\frac{\pi}{8}\Bigr) = \frac{2 - \sqrt{2}}{4} \]

(0, 1)#

\((x,y) = (0,1)\) のとき、アリスとボブは \(\alpha = 0\) と \(\beta = -\pi/8\) を選び、それらの基底を重ね合わせることで、次の図が得られます：

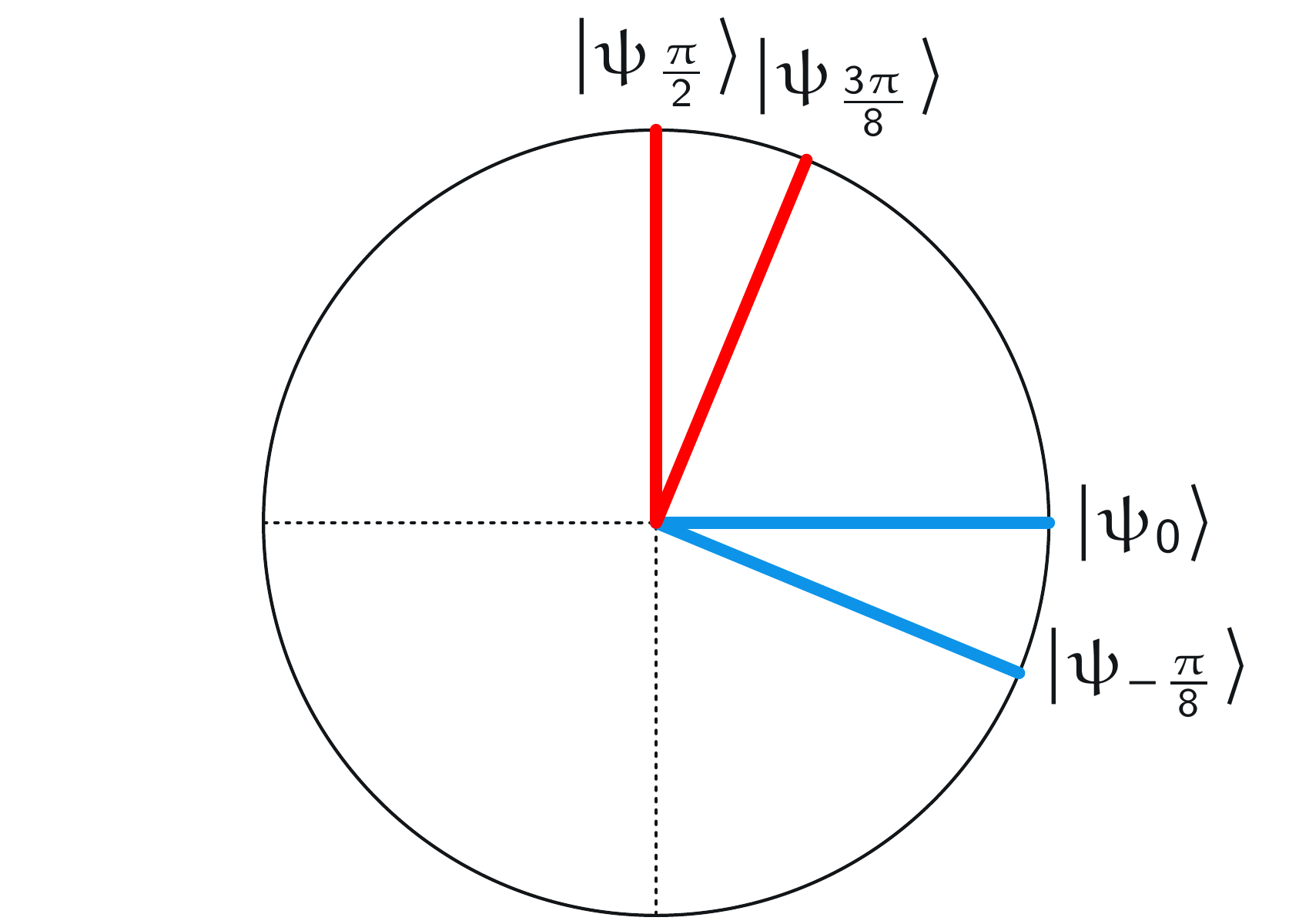
Alice and Bob bases case 1

赤いベクトルの間の角度は同じく \(\pi/8\) であり、これは2つの青いベクトルの間の角度と同じです。アリスとボブの結果が一致する確率は、やはりこの角度の余弦二乗です。

\[ \cos^2\Bigl(\frac{\pi}{8}\Bigr) = \frac{2 + \sqrt{2}}{4}, \]

一方、返答が一致しない確率はこの角度の正弦二乗です。

\[ \sin^2\Bigl(\frac{\pi}{8}\Bigr) = \frac{2 - \sqrt{2}}{4}. \]

(1, 0)#

\((x,y) = (1,0)\) のとき、アリスとボブは \(\alpha = \pi/4\) と \(\beta = \pi/8\) を選び、それらの基底を重ね合わせることで、次の図が得られます：

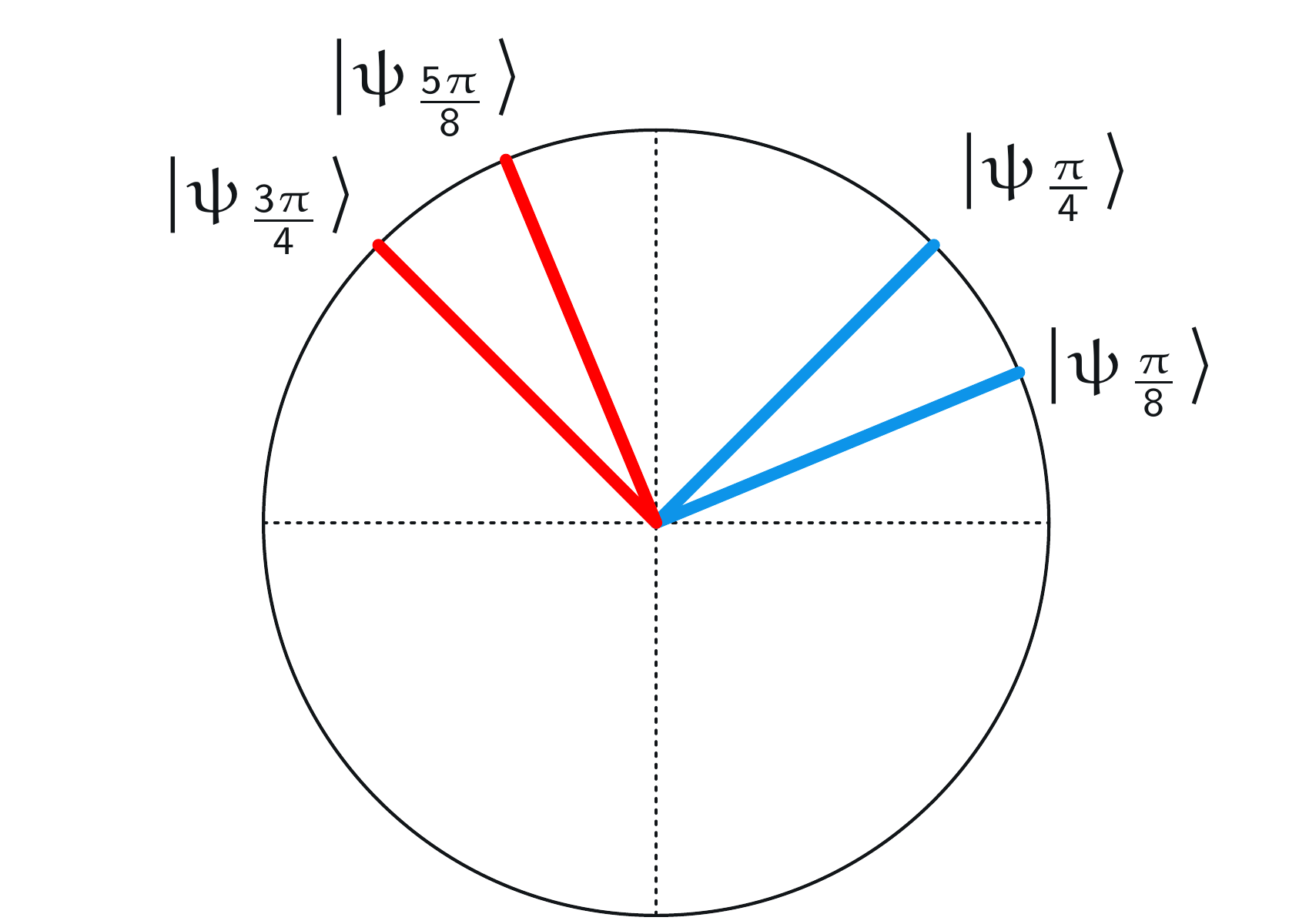
Alice and Bob bases case 1

基底は変わりましたが、角度は変わっていません。先程と同じように、同じ色のベクトル間の角度は \(\pi/8\) です。アリスとボブの結果が一致する確率は

\[ \cos^2\Bigl(\frac{\pi}{8}\Bigr) = \frac{2 + \sqrt{2}}{4} \]

一方、返答が一致しない確率は、

\[ \sin^2\Bigl(\frac{\pi}{8}\Bigr) = \frac{2 - \sqrt{2}}{4} \]

(1, 1)#

\((x,y) = (1,1)\) のとき、アリスとボブは \(\alpha = \pi/4\) と \(\beta = -\pi/8\) を選び、それらの基底を重ね合わせることで、何か違うことが起きているのがわかります：

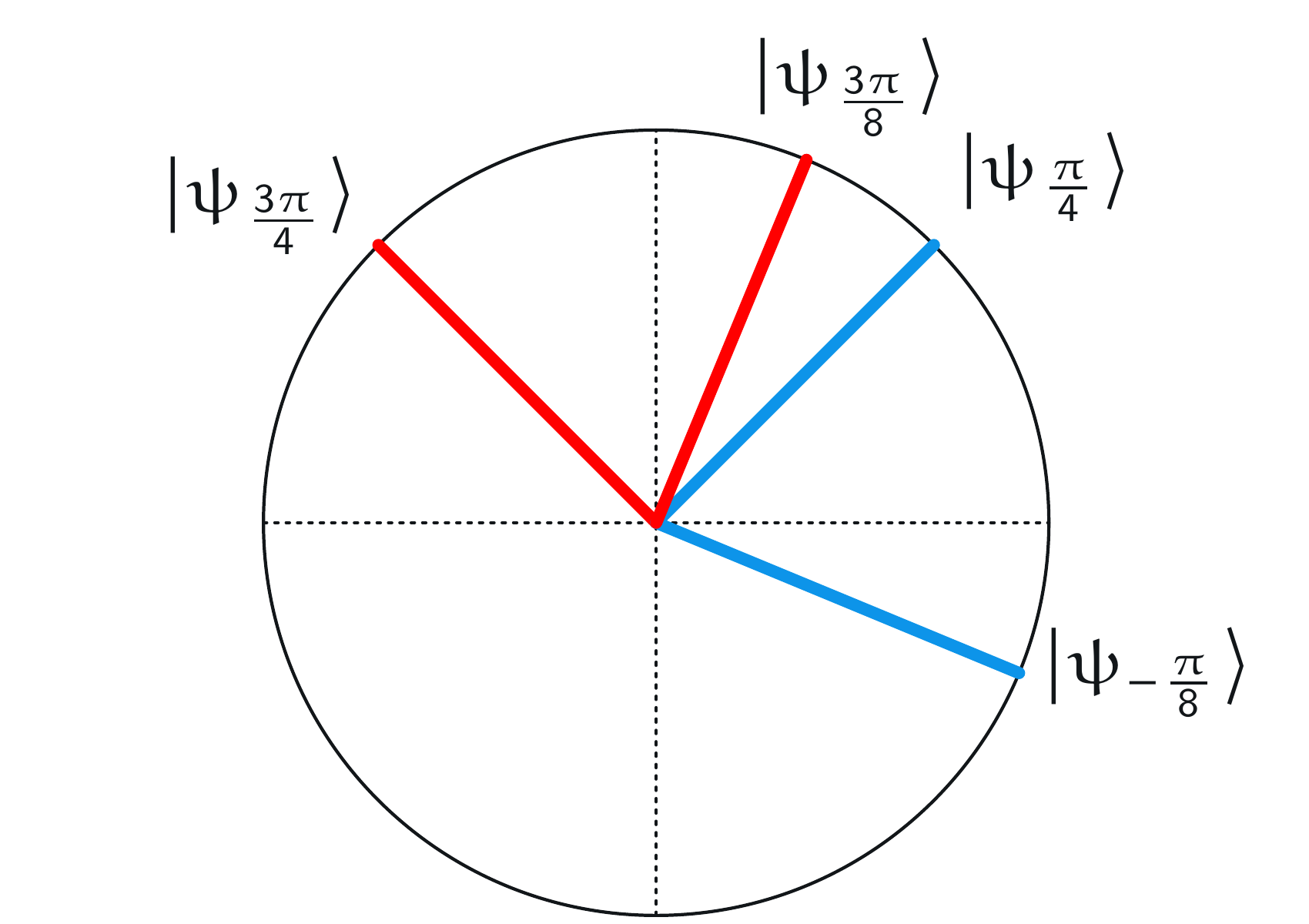
Alice and Bob bases case 1

角度を選んだのですが、今回は同じ色のベクトル同士の角度は \(\pi/8\) ではなく \(3\pi/8\) です。アリスとボブの結果が一致する確率は、この角度の余弦二乗ですが、今回の値は

\[ \cos^2\Bigl(\frac{3\pi}{8}\Bigr) = \frac{2 - \sqrt{2}}{4}. \]

返答が一致しない確率は、この角度の正弦二乗であり、この場合：

\[ \sin^2\Bigl(\frac{3\pi}{8}\Bigr) = \frac{2 + \sqrt{2}}{4}. \]

3.5 備考#

CHSHゲームのように、エンタングルメントによって古典的な記述とは矛盾する統計的な結果が得られるという実験の基本的な考え方は、ベル状態の名付け親であるジョン・ベルによるものです。このため、この種の実験はよくベルテストと呼ばれます。また、ベルの定理と呼ばれることもありますが、これは様々な形で定式化されており、その本質は、量子力学はいわゆる局所隠れ変数理論とは相容れないというものです。CHSHゲームは、ベルテストの非常に優れたきれいな例であり、ベルの定理の証明、あるいは実証と見なすことができます。

CHSHゲームは、量子情報理論が正確な理論であることを実験的に検証するための一つの方法です。CHSHゲームを実装し、上述のエンタングルメントに基づく戦略を検証する実験が可能です。エンタングルメントを説明するために私たちが思いつく、時に曖昧で詩的な方法とは異なり、CHSHゲームはエンタングルメントを観察するための具体的でテストすることの可能な方法を私たちに与えてくれるのです。2022年のノーベル物理学賞は、この分野の重要性が認められました：アラン・アスペクト、ジョン・クラウザー（CHSHのC）、アントン・ザイリンガーが、エンタングルした光子のベルテストによって、エンタングルメントを観測したことについて受賞しました。

3.6 Qiskit での実装#

# Required imports

from qiskit import QuantumCircuit
from qiskit_aer.primitives import Sampler
from numpy import pi
from numpy.random import randint

上記で定義した量子的な戦略でCHSHゲームをQiskitで実装すると、以下のようになります。

まず、これはゲーム自体の定義です。引数として任意の戦略を入れることができます。

def chsh_game(strategy):
    """Plays the CHSH game
    Args:
        strategy (callable): A function that takes two bits (as `int`s) and
            returns two bits (also as `int`s). The strategy must follow the
            rules of the CHSH game.
    Returns:
        int: 1 for a win, 0 for a loss.
    """
    # Referee chooses x and y randomly
    x, y = randint(0, 2), randint(0, 2)

    # Use strategy to choose a and b
    a, b = strategy(x, y)

    # Referee decides if Alice and Bob win or lose
    if (a != b) == (x & y):
        return 1  # Win
    return 0  # Lose

では、アリスとボブの質問に応じた回路を出力する関数を作成します。簡単のために量子ビットの名前はデフォルトのままとし、アリスとボブの行動には組み込みの \(R_y(\theta)\) ゲートを使うことにします。

def chsh_circuit(x, y):
    """Creates a `QuantumCircuit` that implements the best CHSH strategy.
    Args:
        x (int): Alice's bit (must be 0 or 1)
        y (int): Bob's bit (must be 0 or 1)
    Returns:
        QuantumCircuit: Circuit that, when run, returns Alice and Bob's
            answer bits.
    """
    qc = QuantumCircuit(2, 2)
    qc.h(0)
    qc.cx(0, 1)
    qc.barrier()

    # Alice
    if x == 0:
        qc.ry(0, 0)
    else:
        qc.ry(-pi / 2, 0)
    qc.measure(0, 0)

    # Bob
    if y == 0:
        qc.ry(-pi / 4, 1)
    else:
        qc.ry(pi / 4, 1)
    qc.measure(1, 1)

    return qc

どの質問が尋ねられるかに応じて、次の 4 つの回路が考えられます。

# Draw the four possible circuits

print("(x,y) = (0,0)")
display(chsh_circuit(0, 0).draw("mpl"))

print("(x,y) = (0,1)")
display(chsh_circuit(0, 1).draw("mpl"))

print("(x,y) = (1,0)")
display(chsh_circuit(1, 0).draw("mpl"))

print("(x,y) = (1,1)")
display(chsh_circuit(1, 1).draw("mpl"))

(x,y) = (0,0)
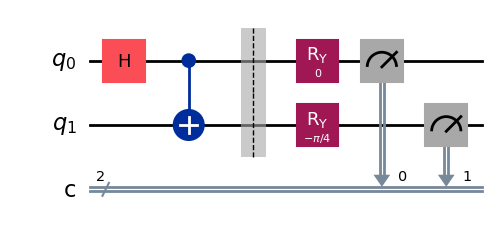
../../_images/7b9806311e071b9a8390b766f8d0638a017d5230dae99fbad2e6db3961f8707b.png 
(x,y) = (0,1)
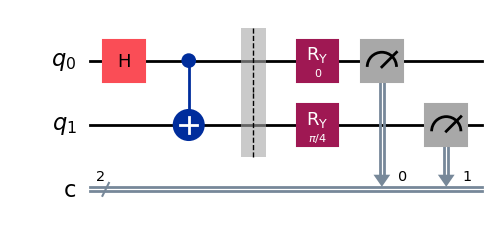
../../_images/33dfc7b4d1b583c09070f2f91772fb0253c9127a943e4c2ed1669005bce665a7.png 
(x,y) = (1,0)
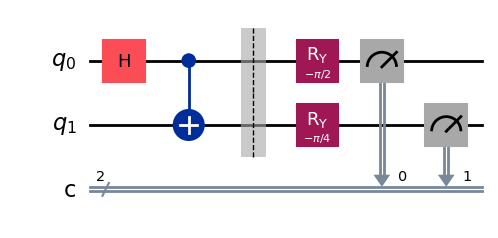
../../_images/ced3372e7c61a220fe655dd9941d9000b46373862f6b5d687f2413348d227b7d.png 
(x,y) = (1,1)
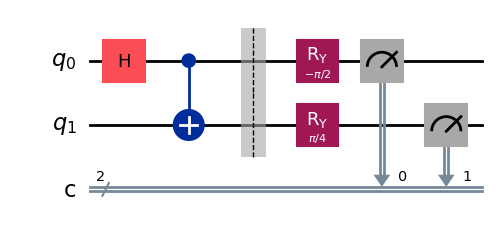
../../_images/fb8539b662ec384edb6f17d8555cfef80c34b0f22e2295a7a8eb5ffdcf8932e6.png

ここで、Aer シミュレーターを使用して特定の入力ペア \((x,y)\) に対して回路を 1 回実行する ジョブを作成します。

sampler = Sampler()


def quantum_strategy(x, y):
    """Carry out the best strategy for the CHSH game.
    Args:
        x (int): Alice's bit (must be 0 or 1)
        y (int): Bob's bit (must be 0 or 1)
    Returns:
        (int, int): Alice and Bob's answer bits (respectively)
    """
    # `shots=1` runs the circuit once
    result = sampler.run(chsh_circuit(x, y), shots=1).result()
    statistics = result.quasi_dists[0].binary_probabilities()
    bits = list(statistics.keys())[0]
    a, b = bits[0], bits[1]
    return a, b

最後に、ゲームを 1,000 回プレイし、この戦略が勝つ割合を計算します。

NUM_GAMES = 1000
TOTAL_SCORE = 0

for _ in range(NUM_GAMES):
    TOTAL_SCORE += chsh_game(quantum_strategy)

print("Fraction of games won:", TOTAL_SCORE / NUM_GAMES)

Fraction of games won: 0.847

また、古典的な戦略を定義し、それがどれほどうまく機能するかを確認することもできます。コードを自由に変更して、さまざまな戦略を試してみてください。

def classical_strategy(x, y):
    """An optimal classical strategy for the CHSH game
    Args:
        x (int): Alice's bit (must be 0 or 1)
        y (int): Bob's bit (must be 0 or 1)
    Returns:
        (int, int): Alice and Bob's answer bits (respectively)
    """
    # Alice's answer
    if x == 0:
        a = 0
    elif x == 1:
        a = 1

    # Bob's answer
    if y == 0:
        b = 1
    elif y == 1:
        b = 0

    return a, b

もう一度、ゲームを 1,000 回プレイして、どれだけうまく機能するか見てみましょう。

NUM_GAMES = 1000
TOTAL_SCORE = 0

for _ in range(NUM_GAMES):
    TOTAL_SCORE += chsh_game(classical_strategy)

print("Fraction of games won:", TOTAL_SCORE / NUM_GAMES)

Fraction of games won: 0.729

ランダム性はありますが、1,000回実行しても統計が大きくずれることはほとんどありません。量子的な戦略では約85％の確率で勝利し、古典戦略では約75％以上の確率で勝利することはできません。