単一システム

はじめに

この授業では、量子情報 の基本的なフレームワークを紹介します。具体的には、複素数の要素を持つベクトルとしての量子状態の記述、量子状態から古典的な情報を抽出できるようにする測定、およびユニタリー行列によって記述される量子状態の操作が含まれます。ここでは、単一のシステムが分離されていると見なされる比較的単純な設定を扱います。この次の授業で、見方を複数のシステムに拡張し、たとえば、複数のシステムが相互に作用し、相互に関連付けられる系について学びます。

実際、量子情報の一般的な数学的記述は 2 つあります。この授業で紹介するのは、そのうちの単純な方です。この記述は、多くの（あるいはほとんどの）量子アルゴリズムを理解するのに十分であり、教育的な観点からも自然な出発点です。

より一般的で、より強力な量子情報の記述である、量子状態を 密度行列 で表現する方法については、後の授業で紹介します。密度行列の記述は、いくつかの理由から、量子情報の研究に不可欠です。例として、 ノイズ の影響をモデル化するために用いることができます。また、量子力学的な計算や、エンタングルしたペアの片方の状態を表すこともできます。密度行列は量子情報理論や量子暗号の数学的な基礎となるものであり、数学的な観点からも非常に美しいものです。これらの理由から、時期が来たらもっと詳しく学ぶことをお勧めしますが、今は簡単な量子情報の記述に焦点を当てます。

1.古典情報

量子情報とその仕組みについて説明するために、まず 古典 情報の概要について説明します。読者の中には、なぜ 量子 情報の講座で古典情報にこれほどまでに注目するのか不思議に思われるかもしれませんが、それにはちゃんとした理由があるのです。一つは、量子情報と古典情報はかなり大きく異なるものの、その数学的記述は実は非常によく似ていることです。

また、古典情報は、量子情報を学ぶ上で身近な存在であり、意外に多くの類似性を持った教材となります。量子情報についての質問には、古典的なアナロジーを持つものがよく出てきます。実際、古典情報を理解せずに量子情報を理解することはできないと主張することは、決して不合理なことではありません。

本章の内容は、既にご存知の方もいらっしゃれば、そうでない方もいらっしゃるかもしれませんが、どちらの方にも楽しんでいただける内容となっています。本章では、量子情報入門に関連する古典的な情報を紹介するとともに、量子情報・計算の分野でベクトルや行列を記述する際によく用いられる ディラック記法 を紹介します。ディラック記法は量子情報に特化した記法ではなく、古典情報の文脈でも、またベクトルや行列が登場する他の多くの場面でも同様に使用することができます。

1.1 古典的な状態と確率ベクトル

情報を格納するシステムがあるとします。より具体的には、このシステムが各時点で有限数の 古典的な状態 のいずれかにあると仮定しましょう。ここで、「古典的な状態」という用語は、直感的に理解できるように、一義的に認識・記述可能な状態を指すものとします。

典型的な例は、古典的な状態が 0 と 1 であるシステムであるビットの例です。他の例には、1、2、3、 4、5、6のある6面ダイス；A 、 C 、 G 、Tである DNAの核酸塩基；高 、 中 、 低 、オフのある扇風機のスイッチなどが古典の状態です。数学的には、システムの古典的状態の指定が出発点となります。古典的状態0と1を持つシステムをビットと定義し、異なる古典的状態セットを持つシステムも同様にビットと定義します。

この議論のために、考慮しているシステムに \(\mathsf{X}\) という名前を付け、記号 \(\class{_sigma}{\Sigma}\) を使用して古典的な状態の集合を記すことにしましょう。\(\mathsf{X}\) の \(\Sigma\) が有限であるという仮定と同様に、前述のように、\(\Sigma\) が空でないことも当然仮定します。物理システムが状態をまったく持たないことは無意味です。無限に多くの古典的な状態を持つ物理システムを考慮することは理にかなっていますが、ここではこの可能性を無視します。限られた数の状態内であっても、探索すべき興味深いアイデアがたくさんあります。便宜上、簡潔にするために、これ以降、 古典状態の集合 という用語を使用して、任意の有限で空でない集合を意味します。

例えば、\(\mathsf{X}\) がビットの場合、\(\Sigma = {0,1}\) (これはよく バイナリー・アルファベット と呼ばれます)であり、; \(\mathsf{X}\) が 6 面ダイスの場合、\(\Sigma = {1,2,3,4,5,6}\) であり、; \(\mathsf{X}\) が扇風機スイッチの場合、\(\Sigma = {\mathrm{high}, \mathrm{medium}, \mathrm{low}, \mathrm{off}}\) です。

\(\mathsf{X}\) を情報の伝達手段として考えると、 \(\mathsf{X}\) のさまざまな古典的な状態に特定の意味が割り当てられ、さまざまな結果や結果につながる可能性があります。そのような場合、 \(\mathsf{X}\) は単に可能な古典的な状態の 1 つにあると説明するだけで十分かもしれません。たとえば、 \(\mathsf{X}\) が扇風機のスイッチである場合、それが high に設定されていることを確実に知ることができます。ただし、情報処理では、 \(\mathsf{X}\) に関する知識が不確実であることがよくあります。 \(\mathsf{X}\) の古典的な状態に関する知識を、それぞれの古典的な状態に 確率的状態 を割り当てることで表します。

たとえば、 \(\mathsf{X}\) がビットだとします。過去に \(\mathsf{X}\) に何が起こったかについて私たちが知っていること、または期待していることに基づいて、おそらく \(\mathsf{X}\) は確率 \(3/4\) の古典的な状態 \(0\) にあり、確率 \(1/4\) で \(1\) の状態にあることを次のように書くことで、その信じている事柄を表すことができます。

\[ \class{probability}{\operatorname{Pr}}(\mathsf{X}=0) = \frac{3}{4} \quad\text{と}\quad \class{probability}{\operatorname{Pr}}(\mathsf{X}=1) = \frac{1}{4}. \]

この確率的状態を表すより簡潔な方法は、列ベクトルを使用することです。

\[\begin{split} \begin{pmatrix} \frac{3}{4}\\[1mm] \frac{1}{4} \end{pmatrix} \end{split}\]

ビットが \(0\) である確率をベクトルの先頭に、ビットが \(1\) である確率を下に配置していますが、これは単に集合 \(\{0,1\}\) の順番で並べるのが通例であるためです。

一般に、古典的な状態集合を持つシステムの確率的な状態は、同じように確率のベクトルとして表現することができます。確率はどのようにでも並べることができ、それは通常、扱う古典的状態集合の自然な並び方やデフォルトの並び方によって決まります。正確には、以下の2つの性質を満たす列ベクトルによって、あらゆる確率的な状態を表現することができます：

1. ベクトルのすべての要素は 非負の実数 です。

2. 要素の合計は \(1\) です。

逆に、これら 2 つの性質を満たす列ベクトルは、確率的状態の表現と見なすことができます。以降、この形式のベクトルを 確率ベクトル と呼ぶことにします。

この表記の簡潔さに加えて、確率的状態を列ベクトルとして表現することで、後述するように確率的状態に対する演算が行列とベクトルの乗算によって表されるという利点があります。

1.2 確率的状態の測定

ここで、あるシステムが確率論的状態にあるときにそれを 測定 するとどうなるかを簡単に考えてみましょう。システムを測定するということは、システムを見て、それがどのような古典的な状態にあるかを明確に認識することを意味します。直感的には、システムを確率的な状態で「見る」ことはできません。測定により、許容される古典的な状態の 1 つが正確に得られます。

測定はシステムに関する知識を変更し、したがってそのシステムに関連付けされた確率的状態を変更します: \(\mathsf{X}\) が古典的な状態 \(a\in\Sigma\) にあると認識した場合、\(\mathsf{X}\) に関する知識を表す新しい確率ベクトルは、 \(a\) に対応する要素が \(1\) で、他のすべての要素が \(0\) のベクトルになります。このベクトルは、 \(\mathsf{X}\) が確実に古典的な状態 \(a\) にあることを示しており、それを認識しただけで知っていることになります。

\(\vert a\rangle\) で、\(a\) に対応する要素に \(1\) を持ち、他のすべての要素に \(0\) を持つベクトルを意味します。このベクトルは「ケット \(a\)」と読みます。理由は後ほど説明します。この種のベクトルは、 標準基底 ベクトルとも呼ばれます。

たとえば、私たちが考えているシステムがビットであると仮定すると、標準基底ベクトルは次のように与えられます。

\[\begin{split} \vert 0\rangle = \begin{pmatrix}1\\0\end{pmatrix} \quad\text{と}\quad \vert 1\rangle = \begin{pmatrix}0\\1\end{pmatrix}. \end{split}\]

任意の2次元列ベクトルは、これら2つのベクトルの線形結合として表現できることに注意してください。例えば次のようになります。

\[\begin{split} \begin{pmatrix} \frac{3}{4}\\[2mm] \frac{1}{4} \end{pmatrix} = \frac{3}{4}\,\vert 0\rangle + \frac{1}{4}\,\vert 1\rangle. \end{split}\]

この事実は当然のことながら、あらゆる古典的な状態の集合に一般化されます。あらゆる列ベクトルは、古典的な状態の線形結合です。ベクトルを標準基底ベクトルの線形結合として表現することは、今後非常に一般的になります。

ここで、測定によって確率的な状態が変化することに話を戻すと、日常の経験と次のようなつながりがあることに気付くかもしれません。例えば、公正なコインを投げ、見る前にコインを覆ったとします。その場合、その確率的状態は次のようになります。

\[\begin{split} \begin{pmatrix} \frac{1}{2}\\[2mm] \frac{1}{2} \end{pmatrix} = \frac{1}{2}\,\vert\text{heads}\rangle + \frac{1}{2}\,\vert\text{tails}\rangle. \end{split}\]

ここで、コインの古典的な状態の集合は \(\{\text{heads},\text{tails}\}\) です。これらの状態を表が先、裏が後の順序となるように並べることにします。

\[\begin{split} \vert\text{heads}\rangle = \begin{pmatrix}1\\0\end{pmatrix} \quad\text{と}\quad \vert\text{tails}\rangle = \begin{pmatrix}0\\1\end{pmatrix} \end{split}\]

コインを取り出して見ると、表または裏の 2 つの古典的な状態のいずれかが表示されるはずです。結果が裏だったと仮定すると、当然、コインの確率的状態の記述を \(|\text{tails}\rangle\) になるように更新します。もちろん、コインを覆い隠し、覆いを取ってもう一度見ると、古典的な状態はやはり裏であり、これはベクトル \(|\text{tails}\rangle\) によって記述される確率的状態と一致します。 これは些細なことのように思えるかもしれませんし、ある意味ではそうです。ただし、量子システムはまったく類似した方法で動作しますが、その測定特性はしばしば普通ではない、または「不気味」と見なされます。古典的なシステムの測定特性を確立することにより、量子情報の類似した動作はそれほど珍しいものではないように見えるかもしれません。

確率的状態の測定に関する最後の注意: それらは知識や信念を説明している可能性があり、必ずしも実際のものとは限りません。コインをひっくり返した後、見る前のコインの状態は、表か裏かのどちらかであり、見るまでどちらかわかりません。見ることで実際に状態が変わるわけではなく、それについての私たちの知識が変わるだけです。古典的な状態が裏であることがわかると、ベクトル \(|\text{tails}\rangle\) をコインに割り当てることによって知識を自然に更新しますが、コインが発見されたときにコインを見なかった他の人には、確率的状態は変わらないままです。これは問題ではありません。個人によって、特定のシステムに関する知識や信念が異なる場合があるため、そのシステムを異なる確率ベクトルで表現することができます。

1.3 古典的な演算

古典的な情報についての簡単な説明の最後に、古典的なシステムに対してどのような演算を行うかについて考えてみましょう。

決定論的演算

まず、 決定論 的な演算があり、各古典的な状態 \(a\in\Sigma\) は、形式 \(f:\Sigma\rightarrow\Sigma\) の関数 \(f\) で \(f(a)\) に変換されます。

たとえば、 \(\Sigma = {0,1}\) の場合、この形式の関数は \(f_1\) 、\(f_2\) 、\(f_3\) 、および \(f_4\) の 4 つあり、次の値の表で表すことができます :

\[\begin{split} \rule[-10mm]{0mm}{15mm} \begin{array}{c|c} a & f_1(a)\\ \hline 0 & 0\\ 1 & 0 \end{array} \qquad \begin{array}{c|c} a & f_2(a)\\ \hline 0 & 0\\ 1 & 1 \end{array} \qquad \begin{array}{c|c} a & f_3(a)\\ \hline 0 & 1\\ 1 & 0 \end{array} \qquad \begin{array}{c|c} a & f_4(a)\\ \hline 0 & 1\\ 1 & 1 \end{array} \end{split}\]

これらの関数のうち、最初のものと最後のものは 定値 です: 各 \(a\in\Sigma\) に対して \(f_1(a) = 0\) と \(f_4(a) = 1\) 。真ん中の 2 つは定値ではなく、 分布 しています。これは、2 つの可能な出力値が、可能な入力の範囲内で同じ回数発生するという意味です。関数 \(f_2\) は 恒等関数 です: 各 \(a\in\Sigma\) に対して \(f_2(a) = a\) 。 \(f_3\) は関数 \(f_3(0) = 1\) および \(f_3(1) = 0\) であり、NOT 関数としてよく知られています。

確率的状態に対する決定論的演算の行為は、行列とベクトルの乗算で表すことができます。具体的には、与えられた関数 \(f:\Sigma\rightarrow\Sigma\) を表す行列 \(M\) は、以下を満たします。

\[ M \vert a \rangle = \vert f(a)\rangle \]

すべての \(a\in\Sigma\) に対して上記を満たします。このような行列は常に存在し、一意です。

たとえば、上記の関数 \(f_1,\ldots,f_4\) に対応する行列 \(M_1,\ldots,M_4\) は次のとおりです。

\[\begin{split} \rule[-6mm]{0mm}{14.5mm} M_1 = \begin{pmatrix} \class{_m00}{1} & \class{_m10}{1}\\ \class{_m01}{0} & \class{_m11}{0} \end{pmatrix}, \hspace{4mm} M_2 = \begin{pmatrix} \class{_m00}{1} & \class{_m10}{0}\\ \class{_m01}{0} & \class{_m11}{1} \end{pmatrix}, \hspace{4mm} M_3 = \begin{pmatrix} \class{_m00}{0} & \class{_m10}{1}\\ \class{_m01}{1} & \class{_m11}{0} \end{pmatrix}, \hspace{4mm} \text{and} \hspace{4mm} M_4 = \begin{pmatrix} \class{_m00}{0} & \class{_m10}{0}\\ \class{_m01}{1} & \class{_m11}{1} \end{pmatrix}. \end{split}\]

決定論的操作を表す行列は、常に各列に 1 つの \(1\) を持ち、他のすべての要素は \(0\) です。

これらの形式やその他の形式の行列を表す便利な方法は、前述の列ベクトルの表記法に類似した行ベクトルの表記法を使用することです。 \(\langle a \vert\) は、各 \(a\in\Sigma\) について、\(a\) に対応する要素が \(1\) で、他のすべての要素がゼロとなる 行 ベクトルを表します。このベクトルは「ブラ \(a\) 」と読みます。

たとえば、\(\Sigma = {0,1}\) の場合、以下のようになります。

\[ \langle 0 \vert = \begin{pmatrix} 1 & 0 \end{pmatrix} \quad\text{と}\quad \langle 1 \vert = \begin{pmatrix} 0 & 1 \end{pmatrix}. \]

古典的な状態集合 \(\Sigma\) の任意の選択に対して、行ベクトルと列ベクトルを行列として表示し、行列乗算 \(\vert b\rangle \langle a\vert\) を実行すると、 \((b,a)\) のペアに対応する要素に \(1\) を含む正方行列が得られます。つまり、要素の行は \(b\) に対応し、列は \(a\) に対応し、他のすべての要素は \(0\) に対応します。例えば、以下のようになります。

\[\begin{split} \vert 0 \rangle \langle 1 \vert = \begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix}. \end{split}\]

この表記法を使用すると、任意の関数 \(f:\Sigma\rightarrow\Sigma\) に対して、関数 \(f\) に対応する行列 \(M\) を次のように表すことができます。

\[ M = \sum_{a\in\Sigma} \vert f(a) \rangle \langle a \vert. \]

ここで、再びベクトルを行列として考えますが、今度は乗算 \(\langle a \vert \vert b \rangle\) を考えると、\(1\times 1\) 行列が得られ、これはスカラー（すなわち数）として考えることができます 。整理して、この積を \(\langle a \vert \vert b \rangle\) ではなく \(\langle a \vert b\rangle\) と書きます。この積は次の簡単な式を満たします。

\[\begin{split} \langle a \vert b \rangle = \begin{cases} 1 & a = b\\ 0 & a \not= b. \end{cases} \end{split}\]

この振る舞いから、行列の乗算が結合的で線形であるという事実とともに、次を得ます。

\[ M \vert b \rangle = \Biggl( \sum_{a\in\Sigma} \vert f(a) \rangle \langle a \vert \Biggr) \vert b\rangle = \sum_{a\in\Sigma} \vert f(a) \rangle \langle a \vert b \rangle = \vert f(b)\rangle, \]

\(b\in\Sigma\) ごとに、これが \(M\) に要求されます。

後に、授業 3 で詳しく説明するように、\(\langle a \vert b \rangle\) は、ベクトル \(\vert a\rangle\) と \(\vert b\rangle\) の間の 内積 と見なすこともできます。内積は量子情報において非常に重要ですが、必要になるまで議論しません。

この時点で、「ブラ」と 「ケット」 という名前が明らかかもしれません: 「ブラ」 \(\langle a\vert\) を 「ケット」 \(\vert b\rangle\) と一緒に置くと、「ブラケット」 \(\langle a \vert b\rangle\) になります。この表記法と用語は ポール・ディラック によるものであり、この理由から ディラック記法 として知られています。

確率演算と確率行列

決定論的演算に加えて、 確率論的演算 があります。

たとえば、ビットの古典的な状態が \(0\) の場合、そのままで、ビットの古典的な状態が \(1\) の場合、 \(1/2\) の確率で \(0\) に反転されるビットの演算を考えてみましょう。 この演算は次の行列で表されます。

\[\begin{split} \begin{pmatrix} 1 & \frac{1}{2}\\[1mm] 0 & \frac{1}{2} \end{pmatrix}. \end{split}\]

標準基底ベクトルを乗算することで、この行列が正しいことを確認できます。

古典状態の集合の任意の選択において、すべての確率演算の集合を、以下の 2 つの特性を満たす行列である 確率 行列によって表される数学用語で説明できます。

1. すべての要素は非負の実数です。

2. すべての列の要素の合計は \(1\)

同様に、確率行列は、すべての列が確率ベクトルを形成する行列です。

上記の例のように、操作中にランダム性が何らかの形で使用または導入される可能性があるものとして、直感的なレベルで確率的演算を考えることができます。確率演算の確率行列の記述に関して、各列は、その列に対応する古典的な状態入力が与えられた場合に生成される確率状態のベクトル表現と見なすことができます。

また、確率行列は、常に確率ベクトルを確率ベクトルにマップする行列であると考えることができます。つまり、確率行列は常に確率ベクトルを確率ベクトルにマッピングするものであり、確率ベクトルを確率ベクトルにマッピングする行列は常に確率行列でなければなりません。

最後に、別の考え方として、確率的演算が決定論的演算のランダムな選択であるといえます。たとえば、上記の例の演算は、恒等関数または定数 0 の関数のいずれかを、それぞれ確率 \(1/2\) で適用すると考えることができます。これは次の式と一致します。

\[\begin{split} \begin{pmatrix} 1 & \frac{1}{2}\\[1mm] 0 & \frac{1}{2} \end{pmatrix} = \frac{1}{2} \begin{pmatrix} 1 & 0\\[1mm] 0 & 1 \end{pmatrix} + \frac{1}{2} \begin{pmatrix} 1 & 1\\[1mm] 0 & 0 \end{pmatrix}. \end{split}\]

このような表現は、古典的な状態の集合と、その古典的な状態の集合で識別される行と列を持つ任意の確率行列の任意の選択に対して常に可能です。

確率演算の合成

\(\mathsf{X}\) が古典的な状態の集合 \(\Sigma\) を持つシステムであり、\(M_1,\ldots,M_n\) がシステム \(\mathsf{X}\) 上の確率的操作を表す確率行列であるとします。

最初の操作 \(M_1\) が確率ベクトル \(u\) で表される確率的状態に適用される場合、結果の確率的状態はベクトル \(M_1 u\) で表されます。次に、2 番目の確率的演算 \(M_2\) をこの新しい確率ベクトルに適用すると以下の確率ベクトルを得ます。

\[ M_2 (M_1 u) = (M_2 M_1) u. \]

この等式は、行列の乗算 (特殊なケースとして行列とベクトルの乗算を含む) が 結合的な 演算であるという事実から得られます。したがって、最初に \(M_1\) を適用し、次に \(M_2\) を適用する 1 番目と 2 番目の確率演算を 合成 することによって得られる確率演算は、行列 \(M_2 M_1\) で表され、これは必然的に確率的です。

より一般的には、行列 \(M_1,\ldots,M_n\) で表される確率演算をこの順序で合成します。つまり、\(M_1\) が最初に適用され、\(M_2\) が 2 番目に適用され、\(M_n\) が最後に適用されることを以下の行列で表します。

\[ M_n \,\cdots\, M_1. \]

ここでは順序が重要であることに注意してください。行列の乗算は合成されますが、一般に 可換 演算ではありません。

たとえば、

\[\begin{split} M_1 = \begin{pmatrix} 1 & 1\\[1mm] 0 & 0 \end{pmatrix} \quad\text{と}\quad M_2 = \begin{pmatrix} 0 & 1\\[1mm] 1 & 0 \end{pmatrix}, \end{split}\]

の場合、以下のようになります。

\[\begin{split} M_2 M_1 = \begin{pmatrix} 0 & 0 \\[1mm] 1 & 1 \end{pmatrix} \quad\text{と}\quad M_1 M_2 = \begin{pmatrix} 1 & 1\\[1mm] 0 & 0 \end{pmatrix}. \end{split}\]

つまり、確率的演算が合成される順序が重要です。合成結合の操作が適用される順序を変更すると、結果の操作が変更される可能性があります。

2. 量子情報

ここで、検討中のシステムの状態 （この場合は 量子状態 ）を表すベクトルの種類について、別の選択を行います。この前の章と同様に、古典的な状態の有限で空でない集合を持つシステムに関係し、前章で導入された表記法の多くを利用します。

2.1 量子状態ベクトル

システムの量子状態は、確率的状態と同様に列ベクトルで表されます。前述のように、ベクトルのインデックスがシステムの古典的な状態にラベルを付けます。量子状態を表すベクトルは、次の 2 つの特性によって特徴付けられます。

1. 量子状態ベクトルの要素は 複素数 です。

2. 量子状態ベクトルの要素の 絶対値の二乗 の合計は \(1\) に等しくなければなりません。

したがって、確率論的な場合とは対照的に、量子状態を表すベクトルは非負の実数の要素を持つ必要はなく、 \(1\) に等しくなければならないのは、(要素の合計ではなく) 要素の絶対値の 2 乗の合計です。この変化は単純ですが、量子情報と古典情報の間にすべての違いが生じます。量子コンピューターによるスピードアップや通信プロトコルの改善は、最終的にはこの単純な数学的変化に由来します。

列ベクトルの ユークリッド ノルム

\[\begin{split} v = \begin{pmatrix} \alpha_1\\ \vdots\\ \alpha_n \end{pmatrix} \end{split}\]

は次のように示され、定義されます。

\[ \| v \| = \sqrt{\sum_{k=1}^n |\alpha_k|^2}. \]

したがって、量子状態ベクトルの絶対値の二乗の合計が \(1\) に等しいという条件は、 \(1\) に等しいユークリッド ノルムを持つベクトルと等価です。つまり、量子状態ベクトルは、ユークリッド ノルムに関する 単位ベクトル です。

量子ビット状態の例

量子ビット という用語は、古典的な状態の集合が \(\{0,1\}\) である量子システムを指します。つまり、量子ビットは実際にはほんの少しですが、この名前を使用することで、私たちはこのビットが量子状態になる可能性があることを明示的に認識しています。

以下は、量子ビットの量子状態の例です。

\[\begin{split} \begin{pmatrix} 1\\[2mm] 0 \end{pmatrix} = \vert 0\rangle \quad\text{と}\quad \begin{pmatrix} 0\\[2mm] 1 \end{pmatrix} = \vert 1\rangle, \end{split}\]

\[\begin{split} \begin{pmatrix} \frac{1}{\sqrt{2}}\\[2mm] \frac{1}{\sqrt{2}} \end{pmatrix} = \frac{1}{\sqrt{2}}\,\vert 0\rangle + \frac{1}{\sqrt{2}}\,\vert 1\rangle, \end{split}\]

\[\tag{1}\]

と $\( \begin{pmatrix} \frac{1+2i}{3}\\[2mm] -\frac{2}{3} \end{pmatrix} = \frac{1+2i}{3}\,\vert 0\rangle - \frac{2}{3}\,\vert 1\rangle. \)$

最初の 2 つの例、 \(\vert 0\rangle\) と \(\vert 1\rangle\) は、標準基底の要素となる量子状態ベクトルであることを示しています：これらの要素は複素数で（この場合の数値の虚数部分はたまたま \(0\) です）、要素の絶対値の二乗の合計を計算すると、

\[ \vert 1\vert^2 + \vert 0\vert^2 = 1 \quad\text{と}\quad \vert 0\vert^2 + \vert 1\vert^2 = 1, \]

が要求されます。古典的な設定と同様に、量子状態ベクトル \(\vert 0\rangle\) および \(\vert 1\rangle\) を、それぞれ古典的な状態 \(0\) または \(1\) にある量子ビットに確実に関連付けます。

他の 2 つの例では、複素数の要素があり、要素の絶対値の 2 乗の和を求めると、次の結果が得られます。

\[ \biggl\vert\frac{1}{\sqrt{2}}\biggr\vert^2 + \biggl\vert\frac{1}{\sqrt{2}}\biggr\vert^2 = \frac{1}{2} + \frac{1}{2} = 1 \]

と

\[ \biggl\vert \frac{1+2i}{3} \biggr\vert^2 + \biggl\vert -\frac{2}{3} \biggr\vert^2 = \frac{5}{9} + \frac{4}{9} = 1. \]

したがって、これらは正しく量子状態ベクトルです。これらは状態 \(\vert 0 \rangle\) と \(\vert 1 \rangle\) の線形結合であることに注意してください。これらの状態は \(0\) 状態と \(1\) 状態の 重ね合わせ であるとよく言います。量子状態のコンテキスト内では、「重ね合わせ」と「線形結合」は本質的に同義です。

上記の量子ビット状態ベクトルの \((1)\) の例は非常によく見られます — これは プラス状態 と呼ばれ、次のように表されます。

\[ \vert + \rangle = \frac{1}{\sqrt{2}} \vert 0\rangle + \frac{1}{\sqrt{2}} \vert 1\rangle. \]

また、以下の表記もあり、

\[ \vert - \rangle = \frac{1}{\sqrt{2}} \vert 0\rangle - \frac{1}{\sqrt{2}} \vert 1\rangle \]

この2 番目の要素が正ではなく負である関連する量子状態ベクトルを マイナス状態 と呼びます。古典的な状態を参照するもの以外の記号がケット内に現れるこの種の表記法は一般的です — ケット内で任意の名前を使用して、ベクトルに名前を付けることができます。

実際、標準基底ベクトルであるとは限らない任意のベクトルを参照するために、 \(\vert\psi\rangle\) のような表記、または \(\psi\) の代わりに他の名前を使用することは非常に一般的です: \(\psi \) は単にベクトルの名前ですが、ベクトルであることを強調する ケット内に置かれます。

ベクトル \(\vert \psi \rangle\) があり、そのインデックスが古典的な状態集合 \(\Sigma\) に対応し、\(a\in\Sigma\) がこの古典的な状態の集合の要素である場合、（行列） 積 \(\langle a\vert \vert \psi\rangle\) は、インデックスが \(a\) に対応するベクトル \(\vert \psi \rangle\) の要素に等しいです。 \(\vert \psi \rangle\) が標準基底ベクトルであるときに行ったように、読みやすさのために \(\langle a\vert \vert \psi\rangle\) ではなく、 \(\langle a \vert \psi \rangle\) と書きます。

たとえば、\(\Sigma = {0,1}\) と

\[\begin{split} \vert \psi \rangle = \frac{1+2i}{3} \vert 0\rangle - \frac{2}{3} \vert 1\rangle = \begin{pmatrix} \frac{1+2i}{3}\\[2mm] -\frac{2}{3} \end{pmatrix}, \end{split}\]

\[ \tag{2}\]

については以下のようになります。

\[ \langle 0 \vert \psi \rangle = \frac{1+2i}{3} \quad\text{と}\quad \langle 1 \vert \psi \rangle = -\frac{2}{3}. \]

この表記法を使うには、\(\langle \psi \vert\) は、列ベクトル \(\vert\psi\rangle\) の 共役転置 を取ることによって得られる行ベクトルを指すことを理解する必要があります。（列ベクトルから行ベクトルへの転置に加えて）各要素はその複素共役に置き換えられます。

たとえば、 \(\vert\psi\rangle\) が \((2)\) で定義されたベクトルである場合、以下のようになります。

\[ \langle\psi\vert = \frac{1-2i}{3} \langle 0\vert - \frac{2}{3} \langle 1\vert = \begin{pmatrix} \frac{1-2i}{3} & -\frac{2}{3} \end{pmatrix}. \]

転置に加えて複素共役を使用する理由は、授業 3 で 内積 について議論すると、より明確になります。

他の系の量子状態

任意の古典的な状態の集合を持つ系の量子状態を考えることができます。

たとえば、扇風機スイッチの量子状態ベクトルは次のとおりです。

\[\begin{split} \begin{pmatrix} \frac{1}{2}\\[1mm] 0 \\[1mm] -\frac{i}{2}\\[1mm] \frac{1}{\sqrt{2}} \end{pmatrix} = \frac{1}{2} \vert\mathrm{high}\rangle - \frac{i}{2} \vert\mathrm{low}\rangle + \frac{1}{\sqrt{2}} \vert\mathrm{off}\rangle. \end{split}\]

ここでの前提は、従来の状態が 高 、 中 、 低 、 オフ の順序になっていることです。扇風機のスイッチの量子状態を考慮したい特別な理由はないかもしれませんが、原理的には可能です。

別の例を次に示します。今回は、古典的な状態が \(0,1,\ldots,9\) である量子 10 進数です。

\[\begin{split} \frac{1}{\sqrt{385}} \begin{pmatrix} 1\\ 2\\ 3\\ 4\\ 5\\ 6\\ 7\\ 8\\ 9\\ 10 \end{pmatrix} = \frac{1}{\sqrt{385}}\sum_{k = 0}^9 (k+1) \vert k \rangle. \end{split}\]

この例は、ディラック記法を使用して状態ベクトルを記述する便利さを示しています。この特定の例では、列ベクトルの表現は面倒であり、古典的な状態がはるかに多い場合は使用できなくなります。対照的に、ディラック記法は、大きくて複雑なベクトルの正確な記述をコンパクトな形式でサポートします。

ディラック記法では、ベクトルのさまざまな側面が 不確定な （未知または未確立を意味する）ベクトルの表現も可能です。たとえば、任意の古典的な状態集合 \(\Sigma\) に対して、量子状態ベクトルを考えることができます。

\[ \frac{1}{\sqrt{|\Sigma|}} \sum_{a\in\Sigma} \vert a \rangle, \]

これは、 \(\Sigma\) の古典的な状態に対する一様な重ね合わせです。（ここで、 \(\vert\Sigma\vert\) という表記は、 \(\Sigma\) の要素数を表します。）

この後の授業では、列ベクトルの使用が非現実的または不可能な量子状態ベクトルのより複雑な表現に遭遇します。実際、要素を明示的に表示して調べることが役立つ場合がある少数の要素を持つベクトル（多くの場合、例にあるようなもの）を除いて、状態ベクトルの列ベクトル表現はほとんど行いません。

ディラック記法を使用して状態ベクトルを表現する方が一般的に便利である理由がもう 1 つあります。それは、古典的な状態の順序付け（または、同等に、古典的な状態とベクトル インデックス間の対応）を明示的に指定する必要性を軽減するためです。たとえば、次のような古典的な状態セット \(\{\clubsuit,\diamondsuit,\heartsuit,\spadesuit\}\) を持つシステムの量子状態ベクトル

\[ \frac{1}{2} \vert\clubsuit\rangle + \frac{i}{2} \vert\diamondsuit\rangle - \frac{1}{2} \vert\heartsuit\rangle - \frac{i}{2} \vert\spadesuit\rangle, \]

はこの式によって明確に記述されており、式を理解するためにこの古典的な状態の集合の順序を選択または指定する必要は実際にはありません。この場合、標準のカードセットの順序を単に指定することは難しくありません。たとえば、 \(\clubsuit\) 、 \(\diamondsuit\) 、 \(\heartsuit\) 、 \(\spadesuit\) のように指定します。この特定の順序を選択すると、上記の量子状態ベクトルは以下の列ベクトルで表されます。

\[\begin{split} \begin{pmatrix} \frac{1}{2}\\[2mm] \frac{i}{2}\\[2mm] -\frac{1}{2}\\[2mm] -\frac{i}{2} \end{pmatrix}. \end{split}\]

ただし、一般的には、古典的な状態の集合がどのように順序付けられているかという問題を無視し、量子状態ベクトルが古典的な状態によって直接インデックス付けされていると見なすのが便利です。

2.2 量子状態の測定

次に、量子状態を 測定 するとどうなるか、 標準基底測定 と呼ばれるシンプルな測定に焦点を当てて考えてみましょう。（後で測定のより一般的な概念を説明します。）

確率論的設定と同様に、量子状態のシステムが測定される場合、測定を実行する観測者は量子状態ベクトルではなく、何らかの古典的な状態を確認します。この意味で、測定は量子情報と古典情報の間のインターフェースとして機能し、それを介して古典情報が量子状態から抽出されます。

ルールは単純です。量子状態が測定される場合、システムの各古典的状態は、その古典的状態に対応する量子状態ベクトルの要素の 絶対値の 2 乗 に等しい確率で得られます。これは、量子力学の ボルン規則 として知られています。このルールは、量子状態ベクトルの要素の絶対値の 2 乗の合計が 1 になるという要件と一致していることに注意してください。これは、さまざまな古典的な状態測定結果の確率の合計が \(1\) になることを意味するためです。

たとえば、プラス状態を測定すると

\[ \vert + \rangle = \frac{1}{\sqrt{2}} \vert 0 \rangle + \frac{1}{\sqrt{2}} \vert 1 \rangle \]

\(0\) と \(1\) の 2 つの結果が得られ、確率は次のようになります。

\[ \operatorname{Pr}(\text{outcome is 0}) = \bigl\vert \langle 0 \vert + \rangle \bigr\vert^2 = \biggl\vert \frac{1}{\sqrt{2}} \biggr\vert^2 = \frac{1}{2} \]

\[ \operatorname{Pr}(\text{outcome is 1}) = \bigl\vert \langle 1 \vert + \rangle \bigr\vert^2 = \biggl\vert \frac{1}{\sqrt{2}} \biggr\vert^2 = \frac{1}{2} \]

興味深いことに、マイナス状態を測定すると

\[ \vert - \rangle = \frac{1}{\sqrt{2}} \vert 0 \rangle - \frac{1}{\sqrt{2}} \vert 1 \rangle \]

2 つの結果の確率はまったく同じになります。

\[ \operatorname{Pr}(\text{outcome is 0}) = \bigl\vert \langle 0 \vert - \rangle \bigr\vert^2 = \biggl\vert \frac{1}{\sqrt{2}} \biggr\vert^2 = \frac{1}{2} \]

\[ \operatorname{Pr}(\text{outcome is 1}) = \bigl\vert \langle 1 \vert - \rangle \bigr\vert^2 = \biggl\vert -\frac{1}{\sqrt{2}} \biggr\vert^2 = \frac{1}{2} \]

これは、標準基底測定に関する限り、プラスとマイナスの状態がまったく同じであることを示唆しています。では、なぜ区別する必要があるのでしょうか。この問題については、次のセクション 2.3 で説明します。

最後の例として、以下の状態の測定

\[ \vert \psi \rangle = \frac{1+2i}{3} \vert 0\rangle - \frac{2}{3} \vert 1\rangle \]

では以下の確率が与えられます。

\[ \operatorname{Pr}(\text{outcome is 0}) = \bigl\vert \langle 0 \vert \psi \rangle \bigr\vert^2 = \biggl\vert \frac{1+2i}{3} \biggr\vert^2 = \frac{5}{9}, \]

と以下です。

\[ \operatorname{Pr}(\text{outcome is 1}) = \bigl\vert \langle 1 \vert \psi \rangle \bigr\vert^2 = \biggl\vert -\frac{2}{3} \biggr\vert^2 = \frac{4}{9}. \]

もちろん、量子状態 \(\vert 0\rangle\) を測定すると確実に古典的状態 \(0\) が得られ、同様に量子状態 \(\vert 1\rangle\) を測定すると確実に古典的状態 \(1\) が得られます。これは、以前に示唆されたように、システムが対応する古典的な状態にあるこれらの量子状態の識別と一致 しています。

2.3 ユニタリー演算

これまでのところ、量子情報が古典的な情報と根本的に異なる理由は明らかではないかもしれません。つまり、量子状態が測定されると、各古典的状態を取得する確率は、対応するベクトルの要素の絶対値の 2 乗で与えられます。では、これらの確率を単純に確率ベクトルに記録してみませんか?

その答えは、少なくとも部分的には、量子状態に対して実行できる一連の許容 操作 が、従来の情報に対するものとは異なるということです。確率論的設定と同様に、量子状態の操作は線形マッピングですが、古典的なケースのように確率行列で表されるのではなく、量子状態ベクトルの操作は ユニタリー 行列で表されます。

複素数の要素を持つ正方行列 \(U\) が、以下の方程式を満たす場合、ユニタリーです。

\[\begin{split} \begin{aligned} U U^{\dagger} &= \class{identity-matrix}{\mathbb{1}} \\ U^{\class{conjugate-transpose}{\dagger}} U &= \class{identity-matrix}{\mathbb{1}}. \end{aligned} \end{split}\]

ここで、 \(\mathbb{1}\) は恒等行列、 \(U^{\dagger}\) は \(U\) の 共役転置 、つまり \(U\) を転置し、各要素の複素共役を取ることによって得られる行列を意味します。
$\( U^{\dagger} = \overline{U^T} \)\( 上記の等式のいずれかが真である場合、もう一方も真でなければなりません。両方の等号は、 \)U^{\dagger}\( が \)U$ の逆行列であることと同等です。

\[ U^{-1} = U^{\dagger}. \]

（警告: \(M\) が正方行列でない場合、 \(M^{\dagger} M = \mathbb{1}\) および \(MM^{\dagger} \not= \mathbb{1}\) である可能性があります。たとえば、上記の最初の方程式の 2 つの等式の等価性は、正方行列の場合にのみ当てはまります。）

\(U\) がユニタリーであるという条件は、 どのベクトルに\(U\) を掛けても、ユークリッド ノルムが変わらないという条件と同じです。つまり、 \(n\times n\) 行列 \(U\) がユニタリーになるのは、すべての \(n\) 次元の列ベクトル \(\vert \psi \rangle\) に対して複素数要素が指定され、 \(\\| U \vert \psi \rangle \\| = \\|\vert \psi \rangle \\|\) の場合だけです。 したがって、すべての量子状態ベクトルの集合は、\(1\) に等しいユークリッド ノルムを持つベクトルの集合と同じであるため、ユニタリー行列を量子状態ベクトルに掛けると、別の量子状態ベクトルが得られます。

実際、ユニタリー行列は、まさに量子状態ベクトルを他の量子状態ベクトルに変換する線形写像の集合です。ここで、確率ベクトルを確率ベクトルに常に変換するものである確率行列に演算が関連付けられている、古典的な確率論的ケースに類似していることに注意してください。

量子ビットへのユニタリー演算の重要な例

以下のリストで、量子ビットに対するいくつかの重要なユニタリー演算について説明します。

1. パウリ演算子 。4 つのパウリ行列は次のとおりです。

   \[\begin{split} \mathbb{1} = \begin{pmatrix} 1 & 0\\ 0 & 1 \end{pmatrix}, \quad \sigma_x = \begin{pmatrix} 0 & 1\\ 1 & 0 \end{pmatrix}, \quad \sigma_y = \begin{pmatrix} 0 & -i\\ i & 0 \end{pmatrix}, \quad \sigma_z = \begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix}. \end{split}\]

   私たちがよく使用する一般的な表記法は、 \(X = \sigma_x\) 、 \(Y = \sigma_y\) 、および \(Z = \sigma_z\) ですが、文字 \(X\)、\(Y\)、および \(Z\) は、他の目的にもよく使用されるので注意してください。 \(\sigma_x\) (または \(X\)) 演算は、ビットに対してこの動作を誘発するため、 ビット フリップ または NOT 演算 とも呼ばれます。

   \[ \sigma_x \vert 0\rangle = \vert 1\rangle \quad \text{と} \quad \sigma_x \vert 1\rangle = \vert 0\rangle. \]

   \(\sigma_z\) (または \(Z\)) 演算は、次のような動作のため、 位相反転 とも呼ばれます。

   \[ \sigma_z \vert 0\rangle = \vert 0\rangle \quad \text{と} \quad \sigma_z \vert 1\rangle = - \vert 1\rangle. \]

2. アダマール演算 。アダマール演算は、次の行列で表されます。

   \[\begin{split} H = \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\[2mm] \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{pmatrix}. \end{split}\]

3. 位相演算 。位相演算は、以下の行列によって記述され、

   \[\begin{split} P_{\theta} = \begin{pmatrix} 1 & 0\\ 0 & e^{i\theta} \end{pmatrix} \end{split}\]

   任意の実数 \(\theta\) に対して演算がなされます。以下の演算

   \[\begin{split} S = P_{\pi/2} = \begin{pmatrix} 1 & 0\\ 0 & i \end{pmatrix} \quad\text{と}\quad T = P_{\pi/4} = \begin{pmatrix} 1 & 0\\ 0 & \frac{1 + i}{\sqrt{2}} \end{pmatrix} \end{split}\]

   は特に重要な例です。他の例には、 \(\mathbb{1} = P_0\) や \(\sigma_z = P_{\pi}\) などがあります。

ここで定義したすべての行列はユニタリーであるため、単一量子ビットに対する量子演算を表します。

たとえば、\(H\) がユニタリーであることを確認する計算は次のとおりです。

\[\begin{split} \begin{aligned} \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\[2mm] \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{pmatrix}^{\dagger} \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\[2mm] \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{pmatrix} & = \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\[2mm] \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{pmatrix} \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\[2mm] \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{pmatrix}\\[2mm] & = \begin{pmatrix} \frac{1}{2} + \frac{1}{2} & \frac{1}{2} - \frac{1}{2}\\[2mm] \frac{1}{2} - \frac{1}{2} & \frac{1}{2} + \frac{1}{2} \end{pmatrix}\\[2mm] & = \begin{pmatrix} 1 & 0\\ 0 & 1 \end{pmatrix}. \end{aligned} \end{split}\]

以下は、量子ビット状態ベクトルに対するアダマール演算の動作例です。

\[\begin{split} \begin{aligned} H \vert 0 \rangle & = \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\[2mm] \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{pmatrix} \begin{pmatrix} 1\\[2mm] 0 \end{pmatrix} = \begin{pmatrix} \frac{1}{\sqrt{2}}\\[2mm] \frac{1}{\sqrt{2}} \end{pmatrix} = \vert + \rangle,\\[2mm] H \vert 1 \rangle & = \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\[2mm] \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{pmatrix} \begin{pmatrix} 0\\[2mm] 1 \end{pmatrix} = \begin{pmatrix} \frac{1}{\sqrt{2}}\\[2mm] -\frac{1}{\sqrt{2}} \end{pmatrix} = \vert - \rangle,\\[2mm] H \vert + \rangle & = \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\[2mm] \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{pmatrix} \begin{pmatrix} \frac{1}{\sqrt{2}}\\[2mm] \frac{1}{\sqrt{2}} \end{pmatrix} = \begin{pmatrix} 1\\[2mm] 0 \end{pmatrix} = \vert 0 \rangle,\\[2mm] H \vert - \rangle & = \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\[2mm] \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{pmatrix} \begin{pmatrix} \frac{1}{\sqrt{2}}\\[2mm] -\frac{1}{\sqrt{2}} \end{pmatrix} = \begin{pmatrix} 0\\[2mm] 1 \end{pmatrix} = \vert 1 \rangle \end{aligned} \end{split}\]

と

\[\begin{split} \begin{aligned} H \biggl(\frac{1+2i}{3} \vert 0\rangle - \frac{2}{3} \vert 1\rangle\biggr) & = \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\[2mm] \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{pmatrix} \begin{pmatrix} \frac{1+2i}{3}\\[2mm] -\frac{2}{3} \end{pmatrix}\\[2mm] & = \begin{pmatrix} \frac{-1+2i}{3\sqrt{2}}\\[2mm] \frac{3+2i}{3\sqrt{2}} \end{pmatrix}\\[2mm] & = \frac{-1+2i}{3\sqrt{2}} | 0 \rangle + \frac{3+2i}{3\sqrt{2}} | 1 \rangle \end{aligned} \end{split}\]

この最後の例は重要ではありませんが、それ以外の例は以下のように、より簡潔に要約する価値があります。

\[\begin{split} \begin{aligned} H \vert 0 \rangle & = \vert + \rangle,\\[2mm] H \vert 1 \rangle & = \vert - \rangle,\\[2mm] H \vert + \rangle & = \vert 0 \rangle,\\[2mm] H \vert - \rangle & = \vert 1 \rangle \end{aligned} \end{split}\]

\(H\vert +\rangle = \vert 0\rangle\) および \(H\vert -\rangle = \vert 1\rangle\) であるという事実をここでストップして考える価値があります。 \(\vert +\rangle\) と \(\vert -\rangle\) の 2 つの量子状態のいずれかで量子ビットが準備されているが、どちらであるかがわからない状況を考えてみましょう。どちらかの状態を測定すると、もう一方と同じ出力分布が生成されます: つまり\(0\) と \(1\) は両方とも等しい確率 \(1/2\) で表示されます。したがって、これでは、元々用意されていた2 つの状態 \(\vert +\rangle\) と \(\vert -\rangle\) のどちらについての情報も提供されません。しかし、アダマール演算を適用して測定すると、元の状態が \(\vert +\rangle\) の場合は確実に結果 \(0\) が得られ、元の状態が \(\vert -\rangle\) の場合は結果 \(1\) が確実に得られます。 したがって、量子状態 \(\vert +\rangle\) と \(\vert -\rangle\) は 完全 に区別できます。これは、量子状態ベクトルの複素数要素の符号の変更、またはより一般的には 位相 (伝統的に 偏角 とも呼ばれる) の変更が、その状態を大幅に変更できることを明らかにしています。

別の例を次に示します。今回は、プラス状態に対する \(T\) 操作の動作です。

\[ T \vert +\rangle = T \biggl(\frac{1}{\sqrt{2}} \vert 0\rangle + \frac{1}{\sqrt{2}} \vert 1\rangle\biggr) = \frac{1}{\sqrt{2}} T\vert 0\rangle + \frac{1}{\sqrt{2}} T\vert 1\rangle = \frac{1}{\sqrt{2}} \vert 0\rangle + \frac{1+i}{2} \vert 1\rangle \]

ここで、同等の行列/ベクトル形式にわざわざ変換せず、代わりに式と一緒に行列乗算の線形性を使用したことに注意してください。

\[ T \vert 0\rangle = \vert 0\rangle \quad\text{and}\quad T \vert 1\rangle = \frac{1 + i}{\sqrt{2}} \vert 1\rangle. \]

同様に、得られたばかりの量子状態ベクトルにアダマール演算を適用した結果を計算できます。

\[\begin{split} \begin{aligned} H\, \biggl(\frac{1}{\sqrt{2}} \vert 0\rangle + \frac{1+i}{2} \vert 1\rangle\biggr) & = \frac{1}{\sqrt{2}} H \vert 0\rangle + \frac{1+i}{2} H \vert 1\rangle\\ & = \frac{1}{\sqrt{2}} \vert +\rangle + \frac{1+i}{2} \vert -\rangle \\ & = \biggl(\frac{1}{2} \vert 0\rangle + \frac{1}{2} \vert 1\rangle\biggr) + \biggl(\frac{1+i}{2\sqrt{2}} \vert 0\rangle - \frac{1+i}{2\sqrt{2}} \vert 1\rangle\biggr)\\ & = \biggl(\frac{1}{2} + \frac{1+i}{2\sqrt{2}}\biggr) \vert 0\rangle + \biggl(\frac{1}{2} - \frac{1+i}{2\sqrt{2}}\biggr) \vert 1\rangle. \end{aligned} \end{split}\]

2 つのアプローチ — 明示的に行列表現に変換する方法と、線形性を使用して標準基底状態での演算の動作をプラグインする方法 — は同等です。その時々の状況に応じて、使いやすいほうを使えばいいのです。

量子ビットユニタリー演算の合成

ユニタリー演算の合成は、確率論の設定で行ったのと同じように、行列の乗算で表されます。たとえば、最初にアダマール演算を適用し、次に \(S\) 演算を適用し、さらに別のアダマール演算を適用すると、結果の演算 (\(R\) と名付けます) は次のようになります。

\[\begin{split} R = H S H = \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\[2mm] \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{pmatrix} \begin{pmatrix} 1 & 0\\ 0 & i \end{pmatrix} \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\[2mm] \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{pmatrix} = \begin{pmatrix} \frac{1+i}{2} & \frac{1-i}{2} \\[2mm] \frac{1-i}{2} & \frac{1+i}{2} \end{pmatrix}. \end{split}\]

このユニタリー演算 \(R\) は興味深い例です。この演算を 2 回適用することで、行列表現を 2 乗することと同等であり、NOT 演算が得られます。

\[\begin{split} R^2 = \begin{pmatrix} \frac{1+i}{2} & \frac{1-i}{2} \\[2mm] \frac{1-i}{2} & \frac{1+i}{2} \end{pmatrix}^2 = \begin{pmatrix} 0 & 1 \\[2mm] 1 & 0 \end{pmatrix}. \end{split}\]

つまり、\(R\) は NOT 演算の平方根 です。同じ演算を 2 回適用して NOT 演算を生成するこのような動作は、単一ビットに対する従来の演算では不可能です。これは、負の数の平方根が実数の線上に留まることはできないという事実に関連しています。

以下の対話型コンポーネントを使用して、一連の量子ビット ユニタリー演算を作成できます。結果のユニタリー演算の行列表現と、状態 \(\vert 0\rangle\) （量子ビットのデフォルトの初期化状態）に対するその動作の両方を示しています。シーケンスを指定するには、量子ビットに実行する演算を下の行にドラッグします。一番左の演算が最初に適用され、一番右の演算が最後に適用されます。この図は 量子回路 を表しており、授業 3 でその詳細と一般性について説明します。

大規模システムでのユニタリー演算

この後の授業では、2 つ以上の古典的な状態を持つシステムでのユニタリー演算の例を多く見ていきます。 3 つの古典的な状態を持つシステムでのユニタリー演算の例は、次の行列によって与えられます。

\[\begin{split} A = \begin{pmatrix} \class{_u00}{0} & \class{_u10}{0} & \class{_u20}{1} \\ \class{_u01}{1} & \class{_u11}{0} & \class{_u21}{0} \\ \class{_u02}{0} & \class{_u12}{1} & \class{_u22}{0} \end{pmatrix} \end{split}\]

システムの古典的な状態が \(0\) 、 \(1\) 、および \(2\) であると仮定すると、この操作は \(3\) を法とする加算として記述できます。

\[ A \vert 0\rangle = \vert 1\rangle, \quad A \vert 1\rangle = \vert 2\rangle, \quad\text{and}\quad A \vert 2\rangle = \vert 0\rangle \]

行列 \(A\) は 置換行列 の例です。これは、すべての行と列に \(1\)が 1 つだけ含まれる行列です。このような行列は、作用するベクトルのエントリを再配置または置換するだけです。単位行列は最も単純な置換行列です。もう 1 つの例は、ビットまたは量子ビットに対する NOT 操作です。すべての置換行列は、任意の正の整数次元でユニタリーです。これらは、古典演算と量子演算の両方を表す行列の唯一の例です。行列は、置換行列である場合に限り、確率論的かつユニタリーです。

ユニタリー行列の別の例、 \(4\times 4\) 行列は次のとおりです。

\[\begin{split} U = \frac{1}{2} \begin{pmatrix} 1 & 1 & 1 & 1 \\ 1 & i & -1 & -i \\ 1 & -1 & 1 & -1 \\ 1 & -i & -1 & i \end{pmatrix}. \end{split}\]

この行列は、特に \(4\times 4\) の場合の 量子フーリエ変換 として知られる操作を表しています。量子フーリエ変換は、任意の正の整数次元 \(n\) に対してより一般的に定義でき、量子アルゴリズムのユニット 2 で重要な役割を果たします。

3. Qiskit コード例

このセクションでは、この授業で紹介した概念の Qiskit 実装の例をいくつか紹介します。

3.1 Python でのベクトルと行列

Qiskit は Python プログラミング言語を使用するため、Qiskit について具体的に説明する前に、Python での行列とベクトルの計算について簡単に説明しておくと役立つ場合があります。 Python では、 NumPy ライブラリー (数値計算用の多くの追加コンポーネントが含まれています) の array クラスを使用して、行列とベクトルの計算を実行できます。

以下は、量子ビット状態ベクトル \(\vert 0\rangle\) と \(\vert 1\rangle\) に対応する 2 つのベクトル ket0 と ket1 を定義し、それらの平均を表示するコード セルの例です。

from numpy import array

ket0 = array([1, 0])
ket1 = array([0, 1])

display(ket0/2 + ket1/2)

array([0.5, 0.5])

実際には、この計算の結果を表示するために明示的に display コマンドを使用する必要はありません。代わりに、目的の式をコード セルの最後の行として単純に記述し、その出力として返されます。

ket0/2 + ket1/2

array([0.5, 0.5])

このコード セルは、このテキストブックの特定のページでコード セルを連続して実行すると累積的な効果があることも示しているため、 array クラスを再読み込みしたり、 ket0 と ket1 を再度定義したりする必要はありません。ただし、ページをリロードしたり、別のページに切り替えたりすると、すべてが初期状態にリセットされます。

一般的なガイドラインとして、このコースの番号が付けられた各サブセクション内のコード セルは、順番に実行されることを意図しています。そのため、コード セルを実行してエラーが発生する場合は、そのコード セルが表示されるサブセクション内の以前のすべてのコード セルを先に最初から実行してください。

array を使用して、操作を表す行列を作成することもできます。

M1 = array([[1, 1], [0, 0]])
M2 = array([[1, 1], [1, 0]])

M1/2 + M2/2

array([[1. , 1. ],
       [0.5, 0. ]])

行列の乗算 (特殊なケースとして行列とベクトルの乗算を含む) は、 NumPy の matmul 関数を使用して実行できます。

from numpy import matmul

display(matmul(M1,ket1))
display(matmul(M1,M2))
display(matmul(M2,M1))

array([1, 0])

array([[2, 1],
       [0, 0]])

array([[1, 1],
       [1, 1]])

3.2 Qiskit での状態、測定、および操作

Qiskit には、状態、測定、および操作を簡単に作成および操作できるいくつかのクラスが含まれています。したがって、ゼロから始めて、Python で量子状態、測定、および操作をシミュレートするために必要なすべてをプログラミングする必要はありません。開始するためのいくつかの例を以下に示します。

状態ベクトルの定義と表示

Qiskit の Statevector クラスは、量子状態ベクトルを定義および操作するための機能を提供します。次のコード セルは Statevector クラスをインポートし、それを使用していくつかのベクトルを定義します。

from qiskit.quantum_info import Statevector
from numpy import sqrt

u = Statevector([1/sqrt(2), 1/sqrt(2)])
v = Statevector([(1+2.j)/3, -2/3])
w = Statevector([1/3, 2/3])

print("State vectors u, v, and w have been defined.")

State vectors u, v, and w have been defined.

(ベクトル u の平方根を計算するには、 NumPy ライブラリーの sqrt 関数が必要であることに注意してください。)

Statevector クラスは、次のコード セルが示すように、さまざまな視覚化のための latex および text オプションを含む、状態ベクトルを表示するための draw メソッドを提供します。

display(u.draw('latex'))
display(v.draw('text'))

\[\frac{\sqrt{2}}{2} |0\rangle+\frac{\sqrt{2}}{2} |1\rangle\]

[ 0.33333333+0.66666667j,-0.66666667+0.j        ]

Statevector クラスには is_valid メソッドも含まれています。このメソッドは、指定されたベクトルが有効な量子状態ベクトルであるかどうか (つまり、ユークリッド ノルムが 1 に等しいかどうか) を確認します。

display(u.is_valid())
display(w.is_valid())

True

False

Statevector を使用した測定のシミュレーション

次に、 Statevector クラスの measure メソッドを使用して、Qiskit で量子状態の測定をシミュレートする方法を見ていきます。

まず、量子ビット状態ベクトル v を作成して表示します。

v = Statevector([(1+2.j)/3, -2/3])
v.draw('latex')

\[(\frac{1}{3} + \frac{2 i}{3}) |0\rangle- \frac{2}{3} |1\rangle\]

（注：コード セルは変更できます。必要に応じてベクトルの仕様を変更してください。または、右側のスクラッチパッドを使用してコード セルを試すこともできます。）

次に、 measure メソッドを実行して、標準基底の測定をシミュレートします。その測定の結果と測定後のシステムの新しい量子状態が返ってきます。

v.measure()

(np.str_('1'),
 Statevector([ 0.+0.j, -1.+0.j],
             dims=(2,)))

測定結果は確率的であるため、同じメソッドが異なる結果を返す可能性があります。これを確認するには、セルを数回実行してみてください。

上記で定義された特定のベクトル v の例では、 measure メソッドは、測定が行われた後の量子状態ベクトルを次のように定義します。

\[ \frac{1 + 2i}{\sqrt{5}} \vert 0\rangle \]

(\(\vert 0\rangle\) ではなく) または

\[ - \vert 1\rangle \]

(\(\vert 1\rangle\) ではなく)上記のようになり、測定結果によって異なります。どちらの場合も、実際にはこれらは同等です。一方が他方に単位円上の複素数を掛けたものに等しいため、 グローバル位相が異なる と言われています。この問題については、授業 3 で詳しく説明しますが、現時点では無視しても問題ありません。

余談ですが、 measure メソッドが無効な量子状態ベクトルに適用されると、 Statevector はエラーを投げます。気が向いたら挑戦してみてください！

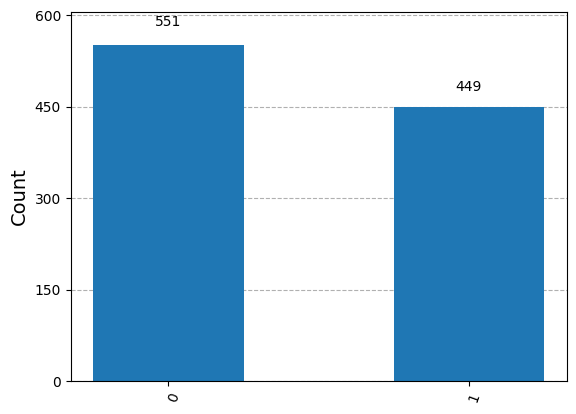
Statevector には、システム上の任意の数の測定のシミュレーションを可能にする sample_counts メソッドも付属しています。たとえば、次のセルはベクトル v を \(1000\) 回測定した結果を示しており、(高い確率で) \(9\) 回ごとに約 \(5\)回 \(0\) の結果となり (または \(1000\) の試行の約 \(556\))、 \(9\) 回ごとに約 \(4\) 回の \(1\) の結果となります(または \(1000\) の試行で約 \(444\) 回) 。このセルは、結果を視覚化するための plot_histogram 関数も示しています。

from qiskit.visualization import plot_histogram

statistics = v.sample_counts(1000)
display(statistics)
plot_histogram(statistics)

{np.str_('0'): np.int64(551), np.str_('1'): np.int64(449)}

\(1000\) の代わりにさまざまな数のサンプルを試すことは、試行回数が推定確率にどのように影響するかについての直感を養うのに役立つ場合があります。

Operator と Statevector を使用した演算の実行

次の例のように、 Operator クラスを使用して Qiskit の状態ベクトルに対してユニタリー演算を定義して実行できます。

from qiskit.quantum_info import Operator

X = Operator([[0,1],[1,0]])
Y = Operator([[0,-1.j],[1.j,0]])
Z = Operator([[1,0],[0,-1]])
H = Operator([[1/sqrt(2),1/sqrt(2)],[1/sqrt(2),-1/sqrt(2)]])
S = Operator([[1,0],[0,1.j]])
T = Operator([[1,0],[0,(1+1.j)/sqrt(2)]])

v = Statevector([1,0])

v = v.evolve(H)
v = v.evolve(T)
v = v.evolve(H)
v = v.evolve(T)
v = v.evolve(Z)

v.draw('text')

[ 0.85355339+0.35355339j,-0.35355339+0.14644661j]

量子回路の先を見据えて

量子回路は授業 3 まで正式に導入されませんが、それでも、Qiskit の QuantumCircuit クラスを使用して量子ビットのユニタリー演算を構成する実験を行うことができます。特に、量子回路 (この場合、単一量子ビットに対して実行されるユニタリー演算のシーケンス) を次のように定義できます。

from qiskit import QuantumCircuit

circuit = QuantumCircuit(1)

circuit.h(0)
circuit.t(0)
circuit.h(0)
circuit.t(0)
circuit.z(0)

circuit.draw("mpl")

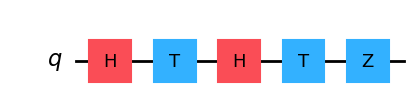
演算操作は、図の左側から順に適用され、右側で終了します。最初に開始量子状態ベクトルを初期化し、次に一連の操作に従ってその状態を進化させましょう。

ket0 = Statevector([1,0])
v = ket0.evolve(circuit)
v.draw('latex')

\[(0.8535533906 + 0.3535533906 i) |0\rangle+(-0.3535533906 + 0.1464466094 i) |1\rangle\]

最後に、この実験 (つまり、状態 \(\vert 0\rangle\) を準備し、回路によって表される演算のシーケンスを適用し、測定する) を 4000 回実行した結果をシミュレートしましょう。

statistics = v.sample_counts(4000)
plot_histogram(statistics)