量子ノイズとエラーの緩和

量子ノイズとエラーの緩和#

Toshinari Itoko (28 June 2024), translated by Kifumi Numata

元の講義のPDFはこちら です。日本語版の講義資料はこちらです。コードはバージョンアップによって、今後動かなくなることがあります。

この実験を実行するためのおおよそのQPU時間は 1 分 40秒です。

1. はじめに#

このレッスンでは、ノイズと、量子コンピューターでノイズを緩和する方法を検討します。まず、実際の量子コンピューターからのノイズプロファイルを使用するなどして、ノイズをシミュレートできるシミュレーターを使用して、ノイズの影響を調べます。次に、実際の量子コンピューターでの固有のノイズに移ります。ゼロノイズ外挿 (zero-noise extrapolation, ZNE) やゲート回転などの組み合わせによるエラー緩和の効果を見ていきます。

はじめに、いくつかのパッケージをロードします。

# !pip install qiskit qiskit_aer qiskit_ibm_runtime
# !pip install jupyter
# !pip install matplotlib pylatexenc

import qiskit

qiskit.__version__

'2.1.2'

import qiskit_aer

qiskit_aer.__version__

'0.17.1'

import qiskit_ibm_runtime

qiskit_ibm_runtime.__version__

'0.41.1'

2. エラー緩和のないノイズのシミュレーション#

Qiskit Aerは、量子コンピューティング用の古典シミュレーターです。理想的な実行だけでなく、ノイズを含めた量子回路の実行もシミュレートできます。このノートブックは、Qiskit Aerを使用してノイズありのシミュレーションを実行する方法を示します。

  1. ノイズモデルを構築する

  2. ノイズモデルでノイズありのsampler(シミュレーター)を構築する

  3. ノイズありのサンプラーで量子回路を実行する

noise_model = NoiseModel()
...
noisy_sampler = Sampler(options={"backend_options": {"noise_model": noise_model}})
job = noisy_sampler.run([circuit])

2.1 テスト回路の構築#

Xゲートを d 回 (d=0 … 100) 繰り返す、1量子ビットの回路を考えます。このトイモデルでオブザーバブル Z を測定します。

from qiskit.circuit import QuantumCircuit

MAX_DEPTH = 100
circuits = []
for d in range(MAX_DEPTH + 1):
    circ = QuantumCircuit(1)
    for _ in range(d):
        circ.x(0)
        circ.barrier(0)
    circ.measure_all()
    circuits.append(circ)

display(circuits[3].draw(output="mpl"))
../../_images/bc032562ec779bf45ff4bcb105990c9f0f464774c6af05d326f18aa73a93edff.png 
from qiskit.quantum_info import SparsePauliOp

obs = SparsePauliOp.from_list([("Z", 1.0)])
obs

SparsePauliOp(['Z'],
              coeffs=[1.+0.j])

2.2 ノイズモデルの構築#

ノイズありのシミュレーションを行うには、NoiseModel を指定する必要があります。このセクションでは、NoiseModel を構築する方法を示します。

まず、ノイズモデルに追加する量子(または読み出し)エラーを定義する必要があります。

from qiskit_aer.noise.errors import (
    coherent_unitary_error,
    amplitude_damping_error,
    ReadoutError,
)
from qiskit.circuit.library import RXGate

# コヒーレント(ユニタリー)エラー: X回転エラー
# https://qiskit.github.io/qiskit-aer/stubs/qiskit_aer.noise.coherent_unitary_error.html#qiskit_aer.noise.coherent_unitary_error
OVER_ROTATION_ANGLE = 0.05
coherent_error = coherent_unitary_error(RXGate(OVER_ROTATION_ANGLE).to_matrix())

# インコヒーレントエラー: 振幅ダンピングエラー
# https://qiskit.github.io/qiskit-aer/stubs/qiskit_aer.noise.amplitude_damping_error.html#qiskit_aer.noise.amplitude_damping_error
AMPLITUDE_DAMPING_PARAM = 0.02  # in [0, 1] (0: no error)
incoherent_error = amplitude_damping_error(AMPLITUDE_DAMPING_PARAM)

# 読み出し(測定)エラー: 読み出しエラー
# https://qiskit.github.io/qiskit-aer/stubs/qiskit_aer.noise.ReadoutError.html#qiskit_aer.noise.ReadoutError
PREP0_MEAS1 = 0.03  # P(1|0): 0を用意したが、1を測定してしまう確率
PREP1_MEAS0 = 0.08  # P(0|1): 1を用意したが、0を測定してしまう確率
readout_error = ReadoutError(
    [[1 - PREP0_MEAS1, PREP0_MEAS1], [PREP1_MEAS0, 1 - PREP1_MEAS0]]
)

from qiskit_aer.noise import NoiseModel

noise_model = NoiseModel()
noise_model.add_quantum_error(coherent_error.compose(incoherent_error), "x", (0,))
noise_model.add_readout_error(readout_error, (0,))

2.3 ノイズモデルを使ったノイズありsamplerの構築#

from qiskit_aer.primitives import SamplerV2 as Sampler

noisy_sampler = Sampler(options={"backend_options": {"noise_model": noise_model}})

2.4 ノイズありsamplerで量子回路を実行#

job = noisy_sampler.run(circuits, shots=400)

result = job.result()

result[0].data.meas.get_counts()

{'0': 386, '1': 14}

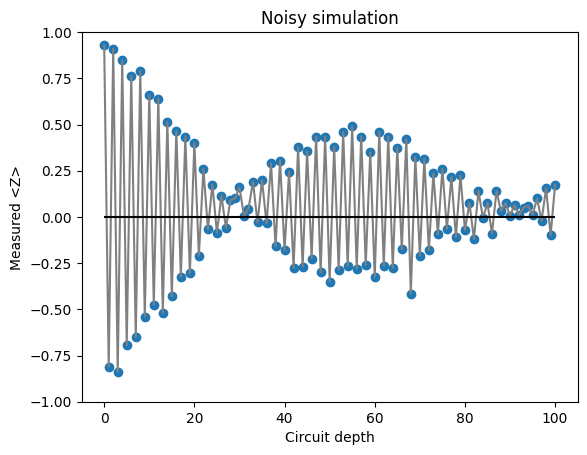
2.5 結果の表示#

import matplotlib.pyplot as plt

plt.title("Noisy simulation")
ds = list(range(MAX_DEPTH + 1))
plt.plot(
    ds,
    [result[d].data.meas.expectation_values(["Z"]) for d in ds],
    color="gray",
    linestyle="-",
)
plt.scatter(ds, [result[d].data.meas.expectation_values(["Z"]) for d in ds], marker="o")
plt.hlines(0, xmin=0, xmax=MAX_DEPTH, colors="black")
plt.ylim(-1, 1)
plt.xlabel("Circuit depth")
plt.ylabel("Measured <Z>")
plt.show()
../../_images/a3d2da0320c17c5183b594865a482492753badd92a0606b37c1758cfbe0ab18f.png

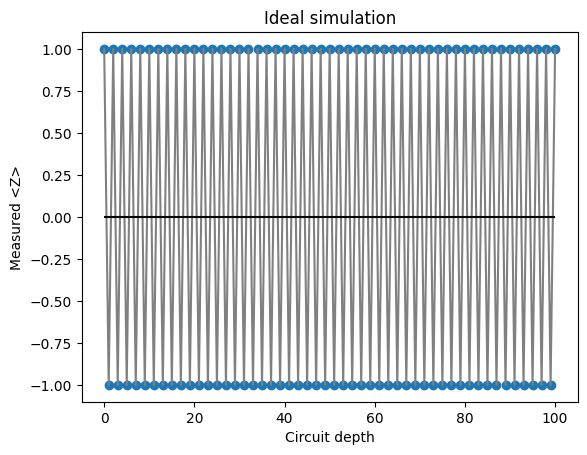
2.6 理想的なシミュレーション#

ideal_sampler = Sampler()
job_ideal = ideal_sampler.run(circuits)
result_ideal = job_ideal.result()
plt.title("Ideal simulation")
ds = list(range(MAX_DEPTH + 1))
plt.plot(
    ds,
    [result_ideal[d].data.meas.expectation_values(["Z"]) for d in ds],
    color="gray",
    linestyle="-",
)
plt.scatter(
    ds, [result_ideal[d].data.meas.expectation_values(["Z"]) for d in ds], marker="o"
)
plt.hlines(0, xmin=0, xmax=MAX_DEPTH, colors="black")
plt.xlabel("Circuit depth")
plt.ylabel("Measured <Z>")
plt.show()
../../_images/2e0164226565335efd4ae30f1b4d5a3bac4feb6657d6534446ad0ef968b98444.png

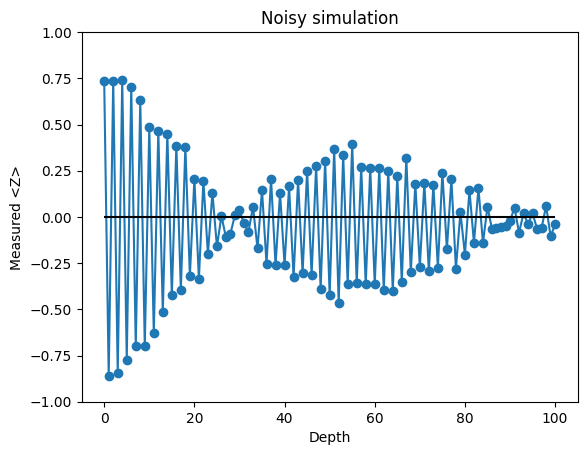
2.7 演習問題#

以下のコードを微調整することで、

  • 25倍のショット数 (10_000 shots) を試して、より滑らかなプロットが得られるようにします

  • ノイズパラメータ(OVER_ROTATION_ANGLE、AMPLITUDE_DAMPING_PARAM、PREP0_MEAS1、またはPREP1_MEAS0)を変更し、プロットがどのように変化するかを確認します

OVER_ROTATION_ANGLE = 0.05
coherent_error = coherent_unitary_error(RXGate(OVER_ROTATION_ANGLE).to_matrix())
AMPLITUDE_DAMPING_PARAM = 0.02  # in [0, 1] (0: no error)
incoherent_error = amplitude_damping_error(AMPLITUDE_DAMPING_PARAM)
PREP0_MEAS1 = 0.1  # P(1|0): 0を用意したが、1を測定してしまう確率
PREP1_MEAS0 = 0.05  # P(0|1): 1を用意したが、0を測定してしまう確率
readout_error = ReadoutError(
    [[1 - PREP0_MEAS1, PREP0_MEAS1], [PREP1_MEAS0, 1 - PREP1_MEAS0]]
)
noise_model = NoiseModel()
noise_model.add_quantum_error(coherent_error.compose(incoherent_error), "x", (0,))
noise_model.add_readout_error(readout_error, (0,))
options = {
    "backend_options": {"noise_model": noise_model},
}
noisy_sampler = Sampler(options=options)
job = noisy_sampler.run(circuits, shots=400)
result = job.result()
plt.title("Noisy simulation")
ds = list(range(MAX_DEPTH + 1))
plt.plot(
    ds,
    [result[d].data.meas.expectation_values(["Z"]) for d in ds],
    marker="o",
    linestyle="-",
)
plt.hlines(0, xmin=0, xmax=MAX_DEPTH, colors="black")
plt.ylim(-1, 1)
plt.xlabel("Depth")
plt.ylabel("Measured <Z>")
plt.show()
../../_images/ff32a10520459dcda39fe02cb710a5cf3e77ae40b0915ab2868fa3614b73ff8f.png

2.8 よりリアルなノイズシミュレーション#

from qiskit_aer import AerSimulator
from qiskit_ibm_runtime import SamplerV2 as Sampler, QiskitRuntimeService

service = QiskitRuntimeService()
real_backend = service.least_busy(
    operational=True, simulator=False, min_num_qubits=127
)  

real_backend

<IBMBackend('ibm_fez')>

aer = AerSimulator.from_backend(real_backend)
noisy_sampler = Sampler(mode=aer)
job = noisy_sampler.run(circuits)
result = job.result()
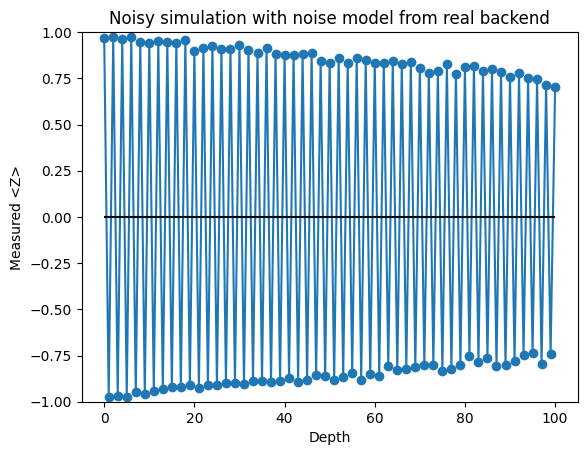
plt.title("Noisy simulation with noise model from real backend")
ds = list(range(MAX_DEPTH + 1))
plt.plot(
    ds,
    [result[d].data.meas.expectation_values(["Z"]) for d in ds],
    marker="o",
    linestyle="-",
)
plt.hlines(0, xmin=0, xmax=MAX_DEPTH, colors="black")
plt.ylim(-1, 1)
plt.xlabel("Depth")
plt.ylabel("Measured <Z>")
plt.show()
../../_images/606e7e626915d0d4a04775848cd7c87a6eeb3c7b8004246b72131259f9f8066f.png

3. エラー緩和を伴った実機による量子計算#

このパートでは、Qiskit Estimatorを使用してエラー緩和された結果(期待値)を取得する方法を示します。 1次元イジングモデルの時間発展をシミュレートするために6量子ビットのトロッター化回路を使って、時間ステップ数に対してエラーがどのようにスケーリングされるかを確認します。

backend = service.least_busy(
    operational=True, simulator=False, min_num_qubits=127
)  
backend

<IBMBackend('ibm_fez')>

NUM_QUBITS = 6
NUM_TIME_STEPS = list(range(8))
RX_ANGLE = 0.1
RZZ_ANGLE = 0.1

3.1 回路の構築#

# 異なるtime steps数で回路を構築する
circuits = []
for n_steps in NUM_TIME_STEPS:
    circ = QuantumCircuit(NUM_QUBITS)
    for i in range(n_steps):
        # rx layer
        for q in range(NUM_QUBITS):
            circ.rx(RX_ANGLE, q)
        # 1st rzz layer
        for q in range(1, NUM_QUBITS - 1, 2):
            circ.rzz(RZZ_ANGLE, q, q + 1)
        # 2nd rzz layer
        for q in range(0, NUM_QUBITS - 1, 2):
            circ.rzz(RZZ_ANGLE, q, q + 1)
    circ.barrier()  # need not to optimize the circuit
    # Uncompute stage
    for i in range(n_steps):
        for q in range(0, NUM_QUBITS - 1, 2):
            circ.rzz(-RZZ_ANGLE, q, q + 1)
        for q in range(1, NUM_QUBITS - 1, 2):
            circ.rzz(-RZZ_ANGLE, q, q + 1)
        for q in range(NUM_QUBITS):
            circ.rx(-RX_ANGLE, q)
    circuits.append(circ)

理想的な出力を事前に知るために、元の回路 \(U\) が適用される第1段階と、それを逆にした \(U^\dagger\) の第2段階から構成される compute-uncompute 回路を使用します。 このような回路の理想的な結果は、入力状態と同じ \(|000000\rangle\) であり、これは、パウリ・オブザーバブルに対してありふれた期待値 (たとえば、\(\langle IIIIIZ \rangle = 1\)) を持つことに注意してください。

# タイムステップ2の回路を表示
circuits[2].draw(output="mpl")
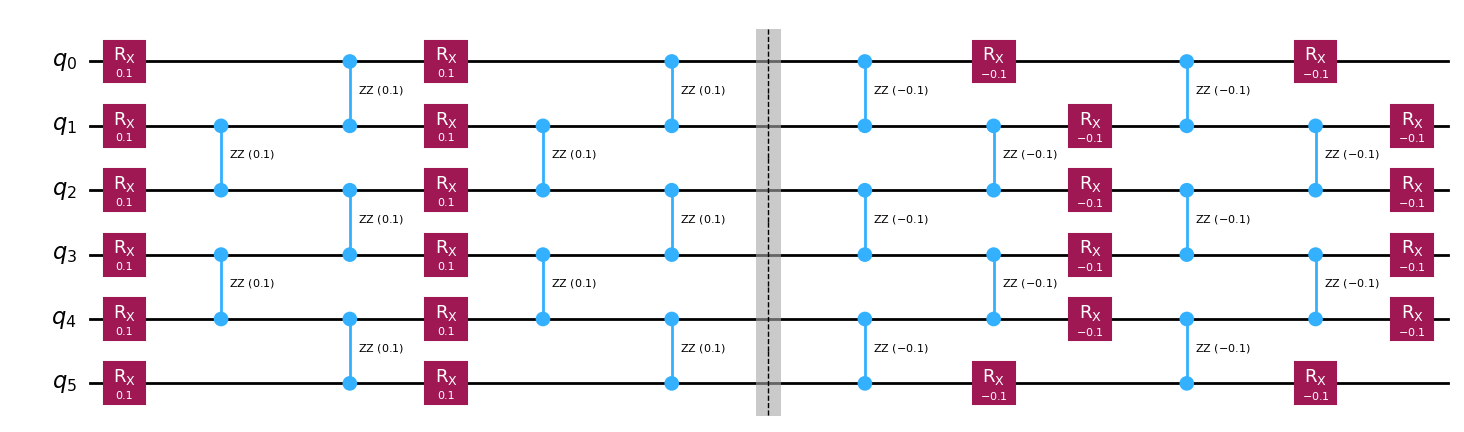
../../_images/3fa77cc8066391f4d4f3119dc52f7e15fe7505350360fcfc1b631b703bd783c0.png

注: 上のように、\(k\) の時間ステップを持つ回路には、\(4k\) 個のの 2 量子ビット・ゲート・レイヤーがあります。

obs = SparsePauliOp.from_sparse_list([("Z", [0], 1.0)], num_qubits=NUM_QUBITS)
obs

SparsePauliOp(['IIIIIZ'],
              coeffs=[1.+0.j])

3.2 回路をトランスパイル#

optimization_level=1 でバックエンドの回路をトランスパイルします。

from qiskit.transpiler.preset_passmanagers import generate_preset_pass_manager

pm = generate_preset_pass_manager(optimization_level=1, backend=backend)
isa_circuits = pm.run(circuits)
display(isa_circuits[2].draw("mpl", idle_wires=False, fold=-1))
../../_images/f456f85e9502421f9930144abda8fe615cbd4fd068cf778bd4ca388be687d89e.png

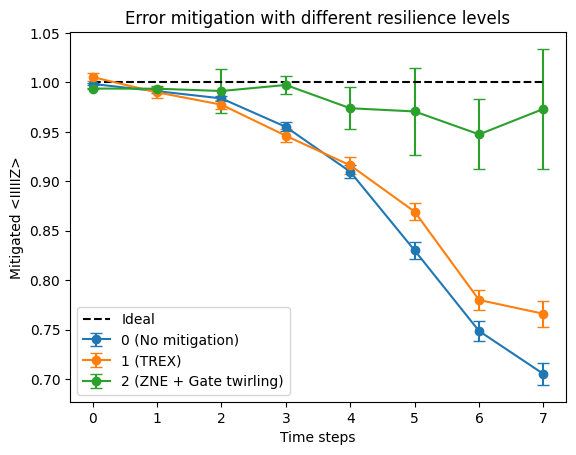
3.3 Estimator を実行 (異なるresilience levelsを用いて)#

resilience level (‘estimator.options.resilience_level’) を設定することは、Qiskit Estimator でエラー緩和を適用する最も簡単な方法です。Estimatorは、以下のresilience levelをサポートしています(2024/06/28時点)。詳細は、 エラー緩和の設定のガイドを参照してください。

Resilience Level

定義

技術

0

緩和なし

なし

1 [デフォルト]

最小限の緩和コスト:読み出しエラーに関連するエラーを緩和

Twirled Readout Error eXtinction (TREX) 測定トワリング

2

程度の緩和コスト。通常、estimator のバイアスを低減しますが、ゼロバイアスであることは保証されません。

Level 1 +ゼロノイズ外挿(ZNE)およびゲートトワリング

 
from qiskit_ibm_runtime import Batch
from qiskit_ibm_runtime import EstimatorV2 as Estimator

jobs = []
job_ids = []
with Batch(backend=backend):
    for resilience_level in [0, 1, 2]:
        estimator = Estimator()
        estimator.options.resilience_level = resilience_level
        job = estimator.run(
            [(circ, obs.apply_layout(circ.layout)) for circ in isa_circuits]
        )
        job_ids.append(job.job_id())
        print(f"Job ID (rl={resilience_level}): {job.job_id()}")
        jobs.append(job)

Job ID (rl=0): d35mmbgitjus73f4gh8g
Job ID (rl=1): d35mmbsgenls73cc69pg
Job ID (rl=2): d35mmbo0sqis7396t40g

# check job status
for job in jobs:
    print(job.status())

DONE
DONE
DONE

# REPLACE WITH YOUR OWN JOB IDS
jobs = [service.job(job_id) for job_id in job_ids]

# Get results
results = [job.result() for job in jobs]

3.4 結果のプロット#

plt.title("Error mitigation with different resilience levels")
labels = ["0 (No mitigation)", "1 (TREX)", "2 (ZNE + Gate twirling)"]
steps = NUM_TIME_STEPS
for result, label in zip(results, labels):
    plt.errorbar(
        x=steps,
        y=[result[s].data.evs for s in steps],
        yerr=[result[s].data.stds for s in steps],
        marker="o",
        linestyle="-",
        capsize=4,
        label=label,
    )
plt.hlines(
    1.0, min(steps), max(steps), linestyle="dashed", label="Ideal", colors="black"
)
plt.xlabel("Time steps")
plt.ylabel("Mitigated <IIIIIZ>")
plt.legend()
plt.show()
../../_images/9bba5b4bc91fa880267fb8856ebed5aa51c7b81fcfbaa50b0d89e6e7392b4eab.png

4. (オプション) エラー緩和オプションのカスタマイズ#

以下に示すように、オプションを使用してエラー緩和手法の適用をカスタマイズできます。

# TREX
estimator.options.twirling.enable_measure = True
estimator.options.twirling.num_randomizations = "auto"
estimator.options.twirling.shots_per_randomization = "auto"

# Gate twirling
estimator.options.twirling.enable_gates = True

# ZNE
estimator.options.resilience.zne_mitigation = True
estimator.options.resilience.zne.noise_factors = [1, 3, 5]
estimator.options.resilience.zne.extrapolator = ("exponential", "linear")

# Dynamical decoupling
estimator.options.dynamical_decoupling.enable = True  # Default: False
estimator.options.dynamical_decoupling.sequence_type = "XX"

# Other options
estimator.options.default_shots = 10_000

エラー緩和オプションの詳細については、次のガイドと API リファレンスを参照してください。

© IBM Corp., 2017-2025

Contents