量子回路における加算器（2019年 Week1）

量子回路における加算器（2019年 Week1）#

この週では、量子回路を用いて単純な古典計算(加算)を行います。

from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit
from qiskit import IBMQ, Aer, execute

基本的な操作と量子ゲート#

量子回路は、量子計算の過程を記述する手法の１つで、基本的な操作を行う量子ゲートを組み合わせて構成されます。まず、いくつかの主要な量子ゲートをご紹介します。

Xゲート#

Xゲートはブロッホ球の\(x\)軸周りの\(\pi\)回転です。 |0>にXゲートを適用すると|1>、|1>にXゲートを適用すると|0>になるので、古典のNOTゲートのような操作が実現でき、ビット反転とも呼ばれます。

\(X = \begin{pmatrix} 0 & 1 \\ 1 & 0 \\ \end{pmatrix}\)

q = QuantumRegister(1)
qc = QuantumCircuit(q)
qc.x(q[0])
qc.draw(output='mpl')
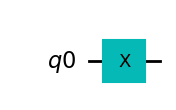
_images/78313c36436bbcb5155f7efbc121ed0a69c81baa75f3c9b11e568e7684d0f5e4.png

Zゲート#

Zゲートはブロッホ球の\(z\)軸周りの\(\pi\)回転です。位相反転とも呼ばれます。

\(Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \\ \end{pmatrix}\)

q = QuantumRegister(1)
qc = QuantumCircuit(q)
qc.z(q[0])
qc.draw(output='mpl')
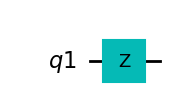
_images/1fcb1b39cc48fb55186c3bf3aff80ec990f2b264507d12d09b7d0b0ceb864236.png

Hゲート#

Hadamardゲート(アダマールゲート)はブロッホ球の\(x\)軸と\(z\)軸の中間の軸周りの\(\pi\)回転です。 例えば|0>にHゲートを適用すると、\(\frac{|0> + |1>}{\sqrt{2}}\)のような重ね合わせ状態を作ることができます。

\(H = \frac{1}{\sqrt{2}}\begin{pmatrix} 1 & 1 \\ 1 & -1 \\ \end{pmatrix}\)

q = QuantumRegister(1)
qc = QuantumCircuit(q)
qc.h(q[0])
qc.draw(output='mpl')
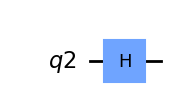
_images/f37056415b0fc6b71d879fc3b994522086fa3442081bd9e34d30095f6b83b69e.png

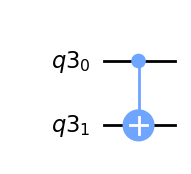
CXゲート(CNOTゲート)#

CXゲートは制御NOTゲート、CNOTとも呼ばれます。CXゲートは、２つの量子ビット(制御量子ビットとターゲット量子ビットと呼びます)を入出力に持ち、制御量子ビットが|1>のときに、ターゲット量子ビットに対してビット反転(Xゲート)を行います。

\(CX = \begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0\\ \end{pmatrix}\)

q = QuantumRegister(2)
qc = QuantumCircuit(q)
qc.cx(q[0],q[1])
qc.draw(output='mpl')
_images/21a98455527b4b4c5057bb523007f406a5261ec06ec8eb47a63bfb9285281b36.png

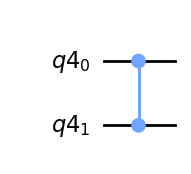
CZゲート#

CZゲートも、２つの量子ビット(制御量子ビットとターゲット量子ビットと呼びます)を入出力に持ち、制御量子ビットが|1>のときに、ターゲット量子ビットに対して位相反転(Zゲート)を行います。

\(CZ = \begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & -1\\ \end{pmatrix}\)

q = QuantumRegister(2)
qc = QuantumCircuit(q)
qc.cz(q[0],q[1])
qc.draw(output='mpl')
_images/bda6486ba382acc07d3ebd83d7b732cfa2c79cac37f7f945a74abf6b24689fb1.png

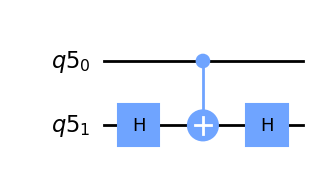
なお、CZゲートはCXゲートとHゲートから作ることができます。

q = QuantumRegister(2)
qc = QuantumCircuit(q)

qc.h(q[1])
qc.cx(q[0],q[1])
qc.h(q[1])
qc.draw(output='mpl')
_images/1ebd3c804b40bde9125e9ed42f4ee6a9f70dd321ad359091339bf07b85e16a04.png

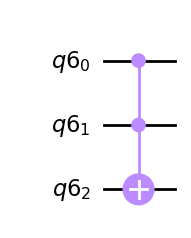
CCXゲート#

CCXゲートはToffoliゲートとも呼ばれます。

CCXゲートは、3つの量子ビット(2つの制御量子ビットと1つのターゲット量子ビット)を入出力に持ち、制御量子ビットが2つとも|1>のときに、ターゲット量子ビットに対してビット反転(Xゲート)を行います。

\(CCX = \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ \end{pmatrix}\)

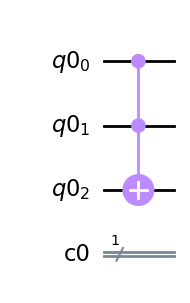
q = QuantumRegister(3)
qc = QuantumCircuit(q)
qc.ccx(q[0],q[1],q[2])
qc.draw(output='mpl')
_images/4c005a77556a08fc7ad361625bcf80229ecd1e4b0502324c12af2dbf943f0f21.png

その他の量子ゲートの詳細に関してはSummary of Quantum Operations をご覧ください。

古典の論理ゲートを量子ゲートで作成する#

古典の論理ゲートを量子ゲートで作成してみましょう。 真理値表と量子回路による表現を以下に示します。なお、量子レジスタをq、古典レジスタをcとし、測定結果を作成する論理ゲートの出力とします。

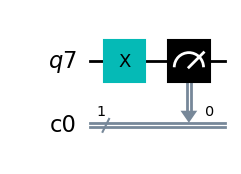
NOTゲート#

先述の通り、XゲートをNOTゲートとみなすことができます。 真理値表は以下のようになります。

入力

出力

0

1

1

0

 
q = QuantumRegister(1)
c = ClassicalRegister(1)
qc = QuantumCircuit(q,c)
qc.x(q[0])
qc.measure(q[0], c[0])
qc.draw(output='mpl')
_images/2cf223cf4f3a20effa3ec12ce63192a902b464b937e83745ce75e34817c5d93e.png

ANDゲート#

ANDゲートの真理値表は以下のようなものです。

入力A

入力B

出力

0

0

0

0

1

0

1

0

0

1

1

1

CCXゲートを用いると、制御量子ビット2つに対するANDゲートの結果をターゲット量子ビットに得られます。

q = QuantumRegister(3)
c = ClassicalRegister(1)
qc = QuantumCircuit(q,c)
qc.ccx(q[0], q[1], q[2])
qc.measure(q[2], c[0])
qc.draw(output='mpl')
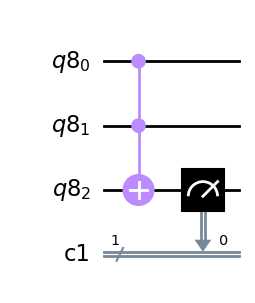
_images/831123a76e2162262bf47f16db6ba9f611bbf277e710c067103048821c3ae10e.png

NANDゲート#

NANDゲートはANDゲートにNOTゲートを適用したものと捉えることができます。

入力A

入力B

出力

0

0

1

0

1

1

1

0

1

1

1

0

 
q = QuantumRegister(3)
c = ClassicalRegister(1)
qc = QuantumCircuit(q,c)
qc.ccx(q[0], q[1], q[2])
qc.x(q[2])
qc.measure(q[2], c[0])
qc.draw(output='mpl')
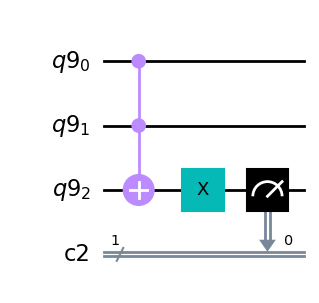
_images/18d05976c2527da3e0fe61a875d84e111e71740bc7712635623cf792d4b5fa71.png

ORゲート#

入力A

入力B

出力

0

0

0

0

1

1

1

0

1

1

1

1

 
q = QuantumRegister(3)
c = ClassicalRegister(1)
qc = QuantumCircuit(q,c)

qc.cx(q[1], q[2])
qc.cx(q[0], q[2])
qc.ccx(q[0], q[1], q[2])
qc.measure(q[2], c[0])
qc.draw(output='mpl')
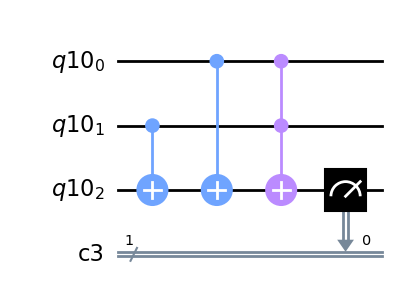
_images/2020f75fceef23c62e911c7bb4612e219c1c7d4daec89cc05c1cf05ed0e5454a.png

XORゲート#

入力A

入力B

出力

0

0

0

0

1

1

1

0

1

1

1

0

 
q = QuantumRegister(3)
c = ClassicalRegister(1)
qc = QuantumCircuit(q,c)
qc.cx(q[1], q[2])
qc.cx(q[0], q[2])
qc.measure(q[2], c[0])
qc.draw(output='mpl')
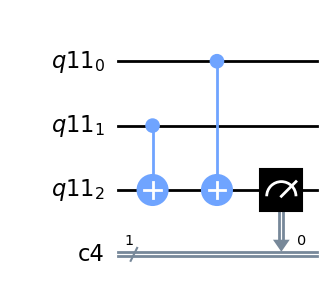
_images/3da071a19b17cbe08ab06570a97d2e14852d574b3e027abf2d09ba83a04f32d6.png

NORゲート#

入力A

入力B

出力

0

0

1

0

1

0

1

0

0

1

1

0

 
q = QuantumRegister(3)
c = ClassicalRegister(1)
qc = QuantumCircuit(q,c)

qc.cx(q[1], q[2])
qc.cx(q[0], q[2])
qc.ccx(q[0], q[1], q[2])
qc.x(q[2])
qc.measure(q[2], c[0])
qc.draw(output='mpl')
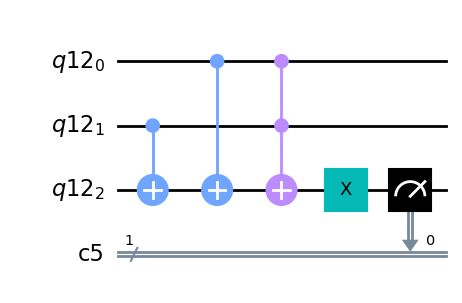
_images/df2ccd99f6c2635b2f938fc9ad6e6213b05d531e42f04c4fa4666349647908d5.png

加算器#

加算器は足し算を行う論理回路です。

今回は最もシンプルな加算器である半加算器と全加算器を用いた加算器に関して考えます。

半加算器#

半加算器は、２進数を2つ与えられたとき、一番下の位の値どうしの加算を行います。 1ビットの情報2つ(入力A,B)が入力として与えられ、桁上げ出力(Carry out)、出力（Sum、和）の２つを出力に持ちます。 この桁上げ出力の情報は、後述の全加算器の入力の１つとして１つ上の位の値を求めるために用いられます。

半加算器は以下の様な真理値表の論理回路で表すことができます。

入力A

入力B

桁上げ出力C

出力S

0

0

0

0

0

1

0

1

1

0

0

1

1

1

1

0

この真理値表を見ると、桁上げ出力Cは入力Aと入力Bに対してANDを適用したものであること、出力Sは入力Aと入力Bに対してXORを適用したものであることがわかります。 ANDとXORに関してはすでに作成済みなので、以下のように組み合わせて半加算器の量子回路が作成できます。

なお、量子レジスタをq, 古典レジスタcとし、入力A, Bをq[0],q[1]に、桁上げ出力C,出力Sをq[2], q[3]に割り振ります。 また、出力結果はc[1], c[0]の順になっていることに注意して下さい。

#各レジスタ、量子回路を宣言
q = QuantumRegister(5)
c = ClassicalRegister(2)
qc = QuantumCircuit(q,c)

#AND
qc.ccx(q[0], q[1], q[2])

qc.barrier(q)

#XOR
qc.cx(q[1], q[3])
qc.cx(q[0], q[3])

qc.barrier(q)

#Carry out
qc.measure(q[2], c[0])
#Sum
qc.measure(q[3], c[1])

backend = Aer.get_backend('qasm_simulator')
job = execute(qc, backend, shots=1000)
result = job.result()
count =result.get_counts()
print(count)
qc.draw(output='mpl')

{'00': 1000}
_images/a6c25535c86b46dc2d5764418a1b715791c0a9540de22a1456266c7f70f09889.png

重要: Unrollerを用いた量子コストの導出#

プログラム(量子回路)を評価する手法がいくつか存在します。

  1. 量子ビット数

  2. 深さ

  3. 実行速度

  4. 命令数

これらはどれも量子計算の結果やスループットなどに影響する重要な尺度ですが、今回のQuantum Challengeでは特に4の命令数を指標として、以下のようにプログラムを評価しています。今回の手法で用いる値をコストと呼称します。

コスト \(=\) 単一量子ビットゲートの数 \(+\) CXゲートの数 \(\times 10\)

任意の量子回路は単一量子ビットゲート(1量子ビットに対する命令)と2量子ビットゲートに対する命令に分解して同等な回路を構築することができます。また、現代のデバイスではCXゲートの方がノイズが乗りやすいので10倍の重み付けをしています。

unrollerと呼ばれるプログラムを用いることで、皆さんのお手元でもこのコストを導出することができます。 例えば、以下のような量子回路があったとします。

import numpy as np
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister
from qiskit import BasicAer, execute
from qiskit.quantum_info import Pauli, state_fidelity, process_fidelity
q = QuantumRegister(4, 'q0')
c = ClassicalRegister(1, 'c0')
qc = QuantumCircuit(q, c)
qc.ccx(q[0], q[1], q[2])
qc.cx(q[3], q[1])
qc.h(q[3])
qc.ccx(q[3], q[2], q[1])
qc.measure(q[3],c[0])
qc.draw(output='mpl')
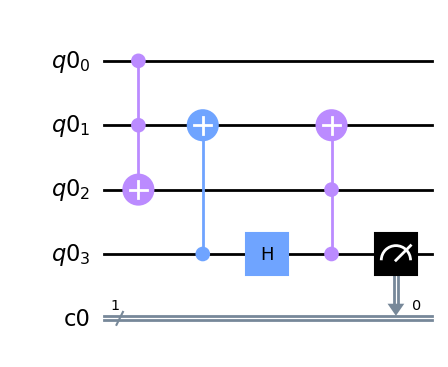
_images/4f0d8fc837c692b2b9ac2597504dbf9f1379664961880af0c2e20cae5988ac0a.png 
qc.count_ops()

OrderedDict([('ccx', 2), ('cx', 1), ('h', 1), ('measure', 1)])

この量子回路には単一量子ビットゲートやCXゲート以外のゲート(CCXゲート)が入っていますが、以下のようにunroller内で指定したゲートのみに分解することができます。

from qiskit.transpiler import PassManager
from qiskit.transpiler.passes import Unroller
pass_ = Unroller(['u3', 'cx'])
pm = PassManager(pass_)
new_circuit = pm.run(qc) 
new_circuit.draw(output='mpl')
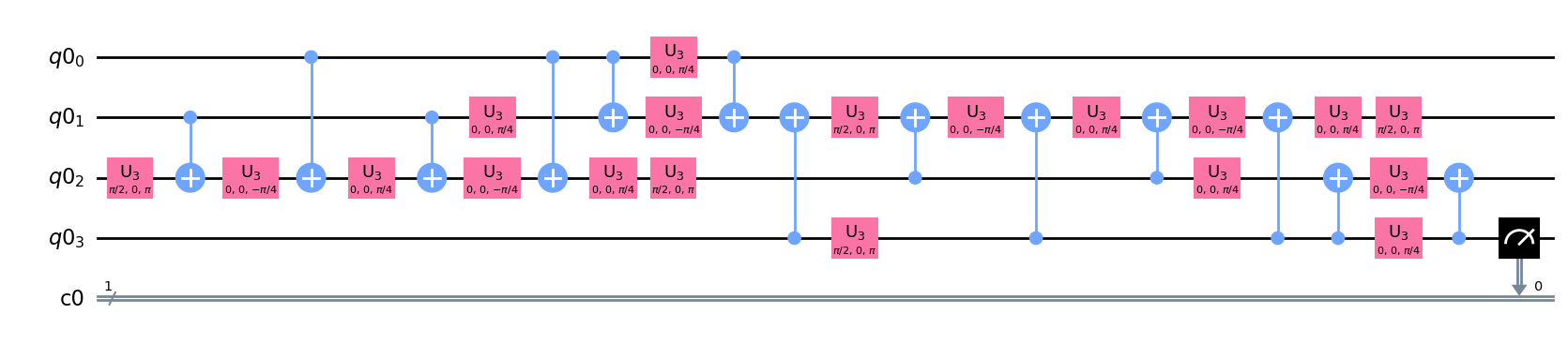
_images/5dc4b0afd3777ee74c992f023d4169b9185c55a79ce3afbacf4c2f02bd8d73ed.png 
new_circuit.count_ops()

OrderedDict([('u3', 19), ('cx', 13), ('measure', 1)])

よって、この回路のコストは\(19+13\times10=149\)ということになります。

単一量子ビットゲートやCXゲート以外のゲートが、Unrollerによってどのように分解されるかは簡単に確認できるので、興味がある人は自分で調べてみましょう。以下ではサンプルとして、CCXゲートを単一量子ビットゲートとCXゲートに分解しています。

q = QuantumRegister(3, 'q0')
c = ClassicalRegister(1, 'c0')
qc = QuantumCircuit(q, c)
qc.ccx(q[0], q[1], q[2])
qc.draw(output='mpl')
_images/3b92e9e2b3c155c56bc1b172ef9b56c23ab1828780ffa24229773a89dd3185c1.png 
pass_ = Unroller(['u3', 'cx'])
pm = PassManager(pass_)
new_circuit = pm.run(qc) 
new_circuit.draw(output='mpl')
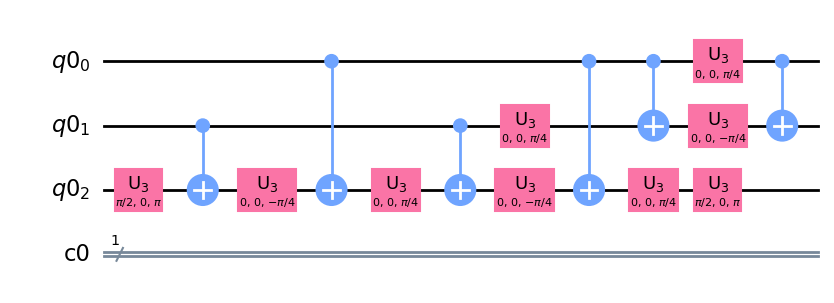
_images/f6223ecba30d583e2a521ae673273ad16b18aacad37443130529a5c4613dc4ab.png 
new_circuit.count_ops()

OrderedDict([('u3', 9), ('cx', 6)])

上記の回路のコストは\(9+6\times10=69\)ということになります。

問題#

全加算器の構築

全加算器は、下の位からの桁上げを含む加算器である。 全加算器を量子回路で表現せよ。なお、真理値表は以下のようになる。

入力A

入力B

桁上げ入力X

桁上げ出力C

出力S

0

0

0

0

0

0

0

1

0

1

0

1

0

0

1

0

1

1

1

0

1

0

0

0

1

1

0

1

1

0

1

1

0

1

0

1

1

1

1

1

なお、量子レジスタをq, 古典レジスタcとする。また、入力A, B, 桁上げ入力Xをそれぞれq[0], q[1], q[2]に与えられるものとし、測定結果のc[0]に桁上げ出力C、c[1]に出力Sが出力されるようにすること。

入力000から111までの出力結果をカンマで区切ったものと、入力000の全加算器に対してunrollerを用いて単一量子ビットゲート(u3)とCXに分解した結果を出力せよ
例
00,01,01,10,01,…改行
u3: 27, cx: 24

解答例1 回路の構築#

#----事前準備----
#各レジスタ、量子回路を宣言
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit
from qiskit import IBMQ, Aer, execute

#Define registers and a quantum circuit
q = QuantumRegister(8)
c = ClassicalRegister(2)
qc = QuantumCircuit(q,c)

# 入力状態の準備（テスト用）
# inputdata = [0,0,0] 
# if inputdata[0] == 0:
#     print('0')
# else: 
#     qc.x(q[0])
#     print('1')
# if inputdata[1] == 0:
#     print('0')    
# else: 
#     qc.x(q[1])
#     print('1')
# if inputdata[2] == 0:
#     print('0')    
# else: 
#     qc.x(q[2])
#     print('1')

#OR
def OR(a,b,c):
    qc.cx(q[b], q[c])
    qc.cx(q[a], q[c])
    qc.ccx(q[a], q[b], q[c])
#半加算器
def hadder(a,b,s,c):
    #XOR
    qc.cx(q[b], q[s])
    qc.cx(q[a], q[s])
    #AND
    qc.ccx(q[a], q[b], q[c])
    
#----ここから処理スタート----

#半加算器1
hadder(0,1,4,3)
qc.barrier(q)
#半加算器2
hadder(4,2,6,5)
qc.barrier(q)
#OR
OR(3,5,7)
qc.barrier(q)
#観測
qc.measure(q[6], c[0])
qc.measure(q[7], c[1])

#----試行結果出力処理----

backend = Aer.get_backend('qasm_simulator')
#作成した回路を1000回動かす
job = execute(qc, backend, shots=1000)
result = job.result()
count =result.get_counts()
#結果の出力
print(count)
qc.draw(output='mpl')

{'00': 1000}
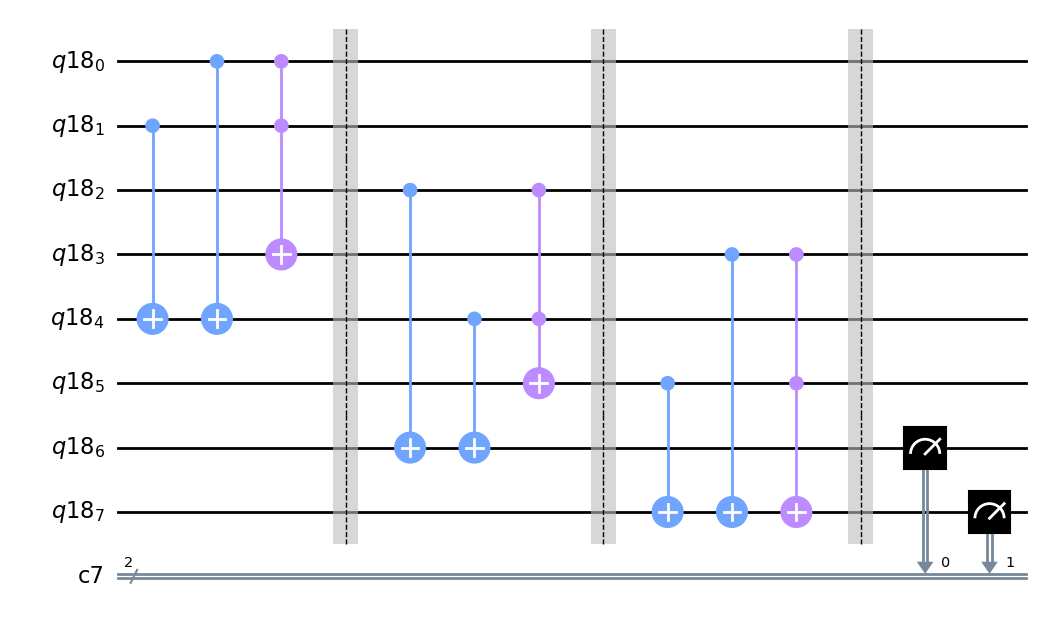
_images/49cb77935abe75f82e805201dd8eaef669558021bf1797270d0f4aaaf7dbb859.png

解説

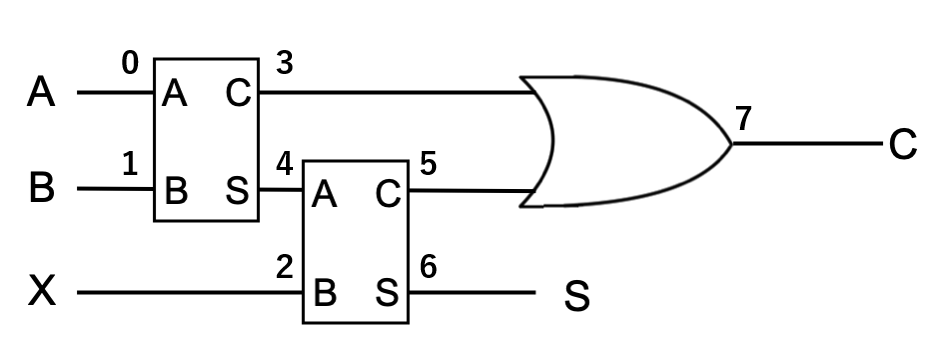
半加算器２つとORを使うことで全加算器を実装することができます。

今回は半加算器とORを関数にしてまとめています。
関数の中身は上で解説済みなので省略します。

—-事前準備—-
古典レジスタ(C, S用の2つ)
量子レジスタ(入出力保存用の8つ)
A, B, Xの入力値を決める(inputdata = [x,x,x]を任意の値にしてif-elseのコメントアウトを全て外す)。
何もしなければA, B, X = 0として処理が動きます。

入力値A, B, Xは量子レジスタの[0], [1], [2]に保持されます。

—-処理の解説—-
処理は左から順番に進めます。

半加算器1では入力値A, Bをそのまま使用します。
そして出力される値C, Sを量子レジスタ[3], [4]に格納します。

次に半加算器2の処理に移ります。
半加算器2に入力される値は前の処理(半加算器1)の出力結果Sと初めの入力値Xです。
量子レジスタのインデックス番号で表すと、[4]と[2]にあたります。
半加算器2の処理結果C, Sをそれぞれ量子レジスタ[5], [6]に格納します。

次に半加算器1の出力結果C([3])と半加算器2の出力結果C([5])をORに渡します。
出力される値を量子レジスタ[7]に格納します。

最後に出力結果C, Sを求めます。
観測する量子レジスタはS:[6],C:[7]です。
観測結果をそれぞれ古典レジスタの[0], [1]に格納します。

—-出力結果の説明—-
左側が出力された値、右側が観測された回数を指します。
例えば{‘00’:1000}と表示された場合は、00という結果が1000回計算されたことを表します

解答例2 出力結果とUnrollerによる分解#

#Unrollerを使って回路をu3とcxゲートに分解してみましょう。
pass_ = Unroller(['u3', 'cx'])
pm = PassManager(pass_)
new_circuit = pm.run(qc) 
new_circuit.draw(output='mpl')

#最後に、量子コストを算出しましょう
new_circuit.count_ops()

OrderedDict([('u3', 27), ('cx', 24), ('barrier', 3), ('measure', 2)])

今回の解答例の量子回路のコストは：\(27+24\times10=267\) となります

Contents